Sensor interface, OP AMP, -500mV +500 mV to 0-5 V amplifier

[Amin Hajihosseinlu]

Hello, I have a signal that is between roughly -500 mV to +500mV, I am trying to boost it to 0 to 5V and connect it to analogue input of the Arduino,
Which OP AMP I should use and how can I shift the voltage to positive side (Arduino does not read negative input).

I appreciate if anybody helps,

Cheers,

 

[Arouse1973]

Hi Amin
So your not worried about the -500 mV then?
Adam

 

[Arouse1973]

Another question. What's the reason you need 0 Volts?
Adam

 

[Amin Hajihosseinlu]

Another question. What's the reason you need 0 Volts?
Adam

Thank you for your quick reply.
It does not have to be 0 volt. Let me explain better,
This voltage (-500mv to +500mv) is coming out of a PH sensor, -500 mv means ph 14 and +500 mv means ph of 0,
I want to give this voltage to analogue input of the Arduino and display the PH,
I was thinking if I can convert -500mv to +500 mv linearly to 0 to 5 v. So in arduiino program, I will know that 0 v means PH of 14 and 5 volt means PH of 0 .

 

[Arouse1973]

So I guess with a zero volt input you are going to want 2.5 Volts out?
Adam

 

[Amin Hajihosseinlu]

So I guess with a zero volt input you are going to want 2.5 Volts out?
Adam

Yes, something like that.
For example, if I could first amplify the voltage (-500mv 500mv) to -2.5v to 2.5v and somehow shift it!?
I am not sure if there is a way to shift the voltage, if there is not, how can I read the negative voltage with the Arduino?

 

[Arouse1973]

Leave it with me and I'll see if I can sort something out for you.
Adam

 

[Arouse1973]

Here is a circuit that does what you want. It's as simple as I can make it. The signal which might need to be buffered is denoted by V2 on the circuit. V3 is an offset voltage which you will need to generate. The signal +V3 is amplified by 10 and then divided by 2 at the output.
Thanks
Adam

 

[Amin Hajihosseinlu]

Here is a circuit that does what you want. It's as simple as I can make it. The signal which might need to be buffered is denoted by V2 on the circuit. V3 is an offset voltage which you will need to generate. The signal +V3 is amplified by 10 and then divided by 2 at the output.
Thanks
Adam
View attachment 23192

Thank you,
Can I increase R1 and R2 to a larger value ?
Let say, instead of 11k and 100 k, make it 110k and 1M?
In order to make the 0.5 volt offset, can I put two large resister in parallel with the 12 V and make a .5 out of it.
For example, puting two resistors (.5Mohm and and 11.5 Mohm ).


Another quick qustion; does the OP AMP have to be LT1366 or any op amp would work? like MCP series
Thanks again.

 

[GPG]

PH sensor

Info on sensor?

 

[Amin Hajihosseinlu]

Info on sensor?

Are you familiar with PH sensors?
I will put the info here tomorrow with a schematic of the sensor.

 

[Arouse1973]

Thank you,
Can I increase R1 and R2 to a larger value ?
Let say, instead of 11k and 100 k, make it 110k and 1M?
In order to make the 0.5 volt offset, can I put two large resister in parallel with the 12 V and make a .5 out of it.
For example, puting two resistors (.5Mohm and and 11.5 Mohm ).


Another quick qustion; does the OP AMP have to be LT1366 or any op amp would work? like MCP series
Thanks again.

You don't need to increase the value of the resistors. A potential divider won't work, you need something to track the voltage to maintain 0.5 Volts above the input. The op-amp can be a different type of course. But you need to make sure it's suitable for working with voltages close to the supply rail (0V). Here is a simple circuit which works by using a current source to supply the 0.5 V offset. I haven't tried this circuit physically so I can't give you any practical results. Also the minus supply could be lower if needed it's just I didn't need it to be -5V but it could be. The op-amp is a dual package in reality so you would be better off either using two independent op-amps or see how it works running both op-amps from a negative supply.
Thanks
Adam

 

[BobK]

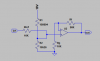
Adam's circuit works, but it is overly complicated and requires a floating supply of 0.5V.

An op amp can sum 2 signals and multiply by a constant all at once. This is done by a summing amplifier.

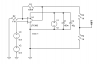
Here is the summing amplifier configuration:



The gain of a non-inverting amp is (1 + Rf / Rg)

And, if we make Rin1 = Rin2, the input at the + input is (in1 + in2) / 2

So, if we make in1 your sensor output (-0.5V to 0.5V) and make in2 0.5V, we get

out = (in1 + 0.5V) / 2 * (1 + Rf / Rg)

We want the output to be 0 to 5V. The minimum of (in1 + 0.5V) / 2 is 0, so that is okay, no offset is needed.
The max of (in1 + 0.5V) / 2 is 0.5V and we want this to come out at 5V, so the gain must be 10.

From the gain equation:

(1 + Rf / Rg) = 10

Rf / Rg = 9

So, choose 90K for Rf and 10K for Rg to get a gain of 10.

Now all we need to do is connect in2 to 0.5V through Rin1.

We can choose any resistance for Rin1 and Rin2 (though they must be the same). I will choose 10K for these.

Now, assuming we have a well regulated supply voltage, all we have to do is find a voltage divider that outputs 0.5V from the supply voltage through a resistance of 10K. Thevenin's theorem allows us to do this.



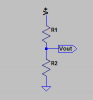
We have two equations that will determine R1 and R2.

The first says that the ratio of R2 to (R1+R2) is the same as the ratio of the output (0.5V) to the input (V):

R2 / (R1 + R2) = 0.5 / V

Flipping both sides:

(R1 + R2) / R2 = V / 0.5 = 2 * V

R1 + R2 = 2 * V * R2

R1 = (2 * V - 1) R2

The second equation states that the parallel combination of R1 and R2 must be 10K:

1 / R1 + 1 / R2 = 1 / 10000

Substituting for R1 from the other equation:

1 / ((2 * V - 1) R2) + 1 / R2) = 1 / 10000

(1 + (1 / (2 * V - 1)) / R2 = 1 /10000

R2 / (1 + (1 / 2 * V - 1)) = 10000

R2 = 10000 * (1 + 1 / (2 * V - 1))

So, if, for example, V is 10:

R2 = 10000 * (1 + 1 / 19) = 10526

And from the equation solved for R1 above:

R1 = (2 * 10 - 1) * 10526 = 199994



So, now the circuit looks like this:

 

[Arouse1973]

Well done Bob. I always forget the good old summing amplifier.
Thanks
Adam

 

[dorke]

remarks to Bob's circuit:
1.connecting the "Ref" voltage in the "location of R2"
creates an undesired effect of lowering the very high input impedance of the previous circuit with in1,in2
2.The above could still be o.k but the "output resistance" of the PH sensor has to be known and be relatively low to the "new" input resistance.
3.In general it is good practice to cancel the effects of input bias currents of the op amp.
(for the LT1366 they are very low-10nA, thus negligible) but for the sake of good design practice...
we need to have:
Rf||Rg =R1||R2||Rin1 ,it can be fixed in the circuit.

 

[dorke]

I would like to add another possibility:
Using a "difference amp" with the LT1366 which is a rail to rail amp.
Thus can be powered with +5V in this "PH sense application"
assuming an accurate +5V it can be used as a "ref"
The circuit inverts the the sensor "logic" ==> 0ph=0v ;14ph=5V.

The input bias can be made close to balanced(0.83/0.91).

Only the resistors ratios are shown,
the values should be chosen according to the PH sensor output resistance.
we can choose R1=100k and calculate the rest.

 

[GPG]

the "output resistance" of the PH sensor has to be known and be relatively low

From reading abt sensors, they are high impedance. The only cct I found uses a CA3140 input buffer. Hence RQ for any data. If a .5v offset on the input is ok then http://www.linear.com/docs/1992 will do the offset and gain.(replacement for the obsolete LM10) If a higher input impedance is required http://ww1.microchip.com/downloads/en/DeviceDoc/21733j.pdf as a buffer
5V single rail compatible

 

[GPG]

And if dual rail needed a switched capacitor converter will do eg:
http://www.analog.com/en/products/p...itor-converters/adm8829.html#product-overview

 

[Arouse1973]

remarks to Bob's circuit:
1.connecting the "Ref" voltage in the "location of R2"
creates an undesired effect of lowering the very high input impedance of the previous circuit with in1,in2
2.The above could still be o.k but the "output resistance" of the PH sensor has to be known and be relatively low to the "new" input resistance.
3.In general it is good practice to cancel the effects of input bias currents of the op amp.
(for the LT1366 they are very low-10nA, thus negligible) but for the sake of good design practice...
we need to have:
Rf||Rg =R1||R2||Rin1 ,it can be fixed in the circuit.

As long as the source driving the input to the op-amp is low enough you don't normally have to worry about input bias current balancing and input offset current. For this technique to work the input currents have to be well matched. For any other op-amp input stage other than the simplest bipolar inputs of op-amps from the 70s, I would suck it and see. You could actually make it worse as most bi-polar op-amps have internal compensation for bias currents now and rail to rail op-amps have complex current paths internally and can reliably only give maximum values.
Thanks
Adam

 

[BobK]

Good comments from GPG. I assumed that since the sensor output -0.5 to 0.5V it was already amplified by an op amp, but apparently not. So a buffer amplifier is required before the summing (or differencing) amp.

One more thing, though:

Even a rail-to-rail amp will not allow the input to go all the way to zero with a single supply. So you should either use dual supplies, or map the range to something not including 0, such as 1-5V if you prefer to use a single supply.

Bob