Most materials are, or can be considered to be ohmic at a single point.
The resistance of a non-ohmic material has to measured at each value of current. The resistance of a ohmic material only has to be measured once.
Ratch
Most materials are, or can be considered to be ohmic at a single point.
J and E define the resistivity and therefore the conductivity. The following is from Wikipedia.
View attachment 33478
Ratch
If V/R is the definition of resistance, then its reciprocal is also the definition of conductivity. Conductivity is just another way of representing a property of a material.I read the Wikipedia article. That does not mean that is the definition of conductivity...
It could be just a constant that Ohm used for his law... And that's what it is. If what you were saying made sense, the same could be said about resistance:
"V=IR is the definition of resistance."
And that's wrong. Constants are used a lot in science to formulate equations. That doesn't mean the equations are the definition of the constant.
Reactance only applies to sinusoidal steady state. Transient behavior requires differential equations. Linear differential equations like those found in most circuits are not too bad.
Good thing we don't live in Columbus's time, or you would believe the Earth is flat. Similarly, in Galileo's time. a lot of folks believed the Earth was the center of the universe.
That is TTT. Charge flows, current is already defined as charge flow. Current flow literally means "charge flow flow". The current into the terminal has the same value as the current leaving the opposite terminal. That is because the same amount of charge accumulating on the capacitor plate per unit time is the same as the amount of charge leaving on the opposite plate per unit time. That does not mean that current exists through the capacitor. If it did, the capacitor would be a resistor.
No it doesn't. There are two circuits involved. One circuit accumulates the charge, the other depletes the charge. The two circuits are isolated from each other by the capacitor's dielectric. The charges that enter a capacitor are not the same charges that leave.
No it doesn't. Circuitwise yes, but on the capacitor itself, no. Kirchoff's law does not apply to a capacitor, because a capacitor stores and dispenses charges.
Mesh analysis works because the capacitor stores and dispenses charge by equal amounts per unit time. This fools a lot of folks into thinking that the current exists through the capacitor. The mathematics of mesh analysis does not know the difference, but those who understand how a capacitor works know what is really happening.
If V/R is the definition of resistance, then its reciprocal is also the definition of conductivity. Conductivity is just another way of representing a property of a material.
Note that the original posting that started this discussion (and which seems to have been lost from this thread) described a problem that was in the sinusoidal steady state, and therefore required only the use of reactance and Ohm's Law (because reactance is measured in ohms) for solution. Only one of a perverse nature would lead the OP along to the unnecessary terrain of transient behavior and differential equations.
There is a well-respected contemporary author whose thesis is, "The World is Flat".
[Current flows. Learn the language or be labeled a stubborn curmudgeon.
Also, if current did not flow through the capacitor dielectric then there would be a discontinuity in the current, and that cannot happen.
That is why Maxwell's equations include a "displacement current" proportional to the rate of change of the electric field in the dielectric. Current flow is not caused only by the movement of charge but also by a changing electric field.
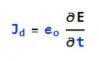
The two "circuits" are not isolated but rather connected by the displacement current.
It can also be said that the charges (electrons) that enter a wire are not the same charges that exit the wire. Ever hear of 'drift velocity' of electrons in a conductor? So tracking the identity of individual charges in a capacitor is a bogus concept.
A capacitor does not store charge. A fully charged capacitor contains no more electric charge than an uncharged capacitor.
Mesh Analysis and Nodal Analysis are unconcerned with what may happen inside a connected device. A resistor, a capacitor, or an inductor are just two-terminal devices having a simple mathematical description of the voltage-current behavior at the two terminals.
Nothing else matters.
That doesn't mean J=σE is not Ohm's law, and is instead, the definition of conductivity.
Look at the OP's first post again. The title of the thread was I = C dv/dt, and he asked how to obtain dv/dt. That is a differential equation question, not a steady state condition.
You want it to be a method of calculation.
"More specifically, Ohm’s law states the following: For many materials (including most metals), the ratio of the current density to the electric field is a constant s that is independent of the electric field producing the current"
7th edition, Vol 2, page 756.
No, sir, I think you made that up. I even quoted the part where it said it is a property. It has a consequence, which is the equation. That doesn't mean that equation is the definition of conductivity (which is what you said). It's just Ohm's law expressed in therms of an equation.
An equation by itself cannot express linearity. Ohm's law requires linearity. The equation has to be analyzed to determine if it is linear. Therefore, an equation by itself cannot express Ohm's law.
it is a property. It has a consequence, which is the equation.
You are just summarizing what I´ve been saying...
I am quoting from a book called Introduction to Electrodynamics, Third Edition, by David J. Griffiths.
"Maxwell called his extra term the displacement current:

It's a misleading name, since it has nothing to do with current, except that it adds to J in Ampere's law."
Do you know what you are talking about?
You should refer to these class notes for a course in Applied Electromagnetics.
http://whites.sdsmt.edu/classes/ee382/notes/382Lecture5.pdf
Then you may be able to understand the following diagram showing displacement current flowing through the dielectric of a capacitor.
View attachment 33545
I read through the notes in the attachment. No where does it say that conduction current exists through the capacitor.
Some sources I have come across call the displacement current a "fictitious" current. It has the units of current, but it is not real current. I see no conflict between the notes and what I averred.
The best explanation I found so far is from Wikipedia, as quoted below. They claim that a magnetic field exists between the capacitor plates equivalent to what the conduction current would generate.
This equivalent magnetic field, when taken into consideration, corrects a discrepancy of Ampere's law. But again, this does not mean that charges pass through the dielectric.
Correct. That is because displacement current is not conduction current.
But what you aver is not the the whole picture. What you aver leads to a discontinuity in the current flow. What you aver is what Maxwell found necessary to correct.
That is because the displacement current is a real current that generates a real magnetic field. In an ideal capacitor the magnitude of the displacement current is equal to the magnitude of the conduction current. That is why "a magnetic field exists between the capacitor plates equivalent to what the conduction current would generate".
This 'discrepancy' is a fundamental property that cannot be ignored. Current flow is not due simply to the movement of charge (conduction current), but is also caused by a time variance in the electric field (displacement current).
Nevertheless, this can be ignored for the purposes of circuit analysis which focuses only on the external terminal behavior of the capacitor. Nothing else matters.
Therefore, charge does not pass through the dielectric.
The cap inputs current and outputs current both at the same time and at the same value. You could say that there is a discontinuity at each plate of the cap, but no net discontinuity exists. Max added the magnetic field term to "fix" Ampere's law. He should not have called that term "displacement current". That was a misnomer. Many authorities agree on that point.
The mag field is not caused by any "fictional" charge moving through the dielectric.
Why not just say current instead of current flow?
The time variance of the electric field causes a mag field to form, but does not generate a current. You can show the mag field is equivalent to what the same value of conduction current would generate, but that fictional current does not exist, and the corrective term should not be called current.
It is ignored because the net discontinuity in a cap does not exist..
You definitively state the obvious. Hmmmm.
When anyone relies on the "Many Authorities Agree" defense, you know they have lost the argument because what that really means is, "While many authorities agree, most authorities do not subscribe to the crackpot proposition being purveyed." Meanwhile, Maxwell has survived the test of time.
That statement is based on an obvious misconception. Displacement current is not caused by the flow of charge. Only conduction current is caused by the flow of charge.
Why not just say "current flow" like everyone else? C'mon, you know you want to!
Maxwell does not agree with you. He called it 'displacement current'. However, when ALL authorities agree that Maxwell is wrong, then you should post the announcement.

Quite irrelevant! It is ignored because in circuit analysis we don't use a 'capacitor', rather we use a mathematical model of an ideal capacitor terminal characteristics.
The fundamental passive components for circuit analysis are the resistor, capacitor, and inductor; each one given as a two terminal device with a mathematical definition relating the current flowing through the device terminals to the voltage existing between the device terminals. Current flows through the device model by definition; you can't argue with a definition.
View attachment 34129
So it becomes patently obvious that circuit analysts should model current flowing through a capacitor without being assaulted by curmudgeons claiming that Maxwell was wrong. Case closed.The definition could not be used if a net discontinuity existed.
