Phase Shift Oscillator

[Excalibur]

Hi everyone, I had to build an oscillator which generates a sinusoidal signal of frequency 5kHz and Vi = 25 mV. I used a phase shift oscillator to achieve this.

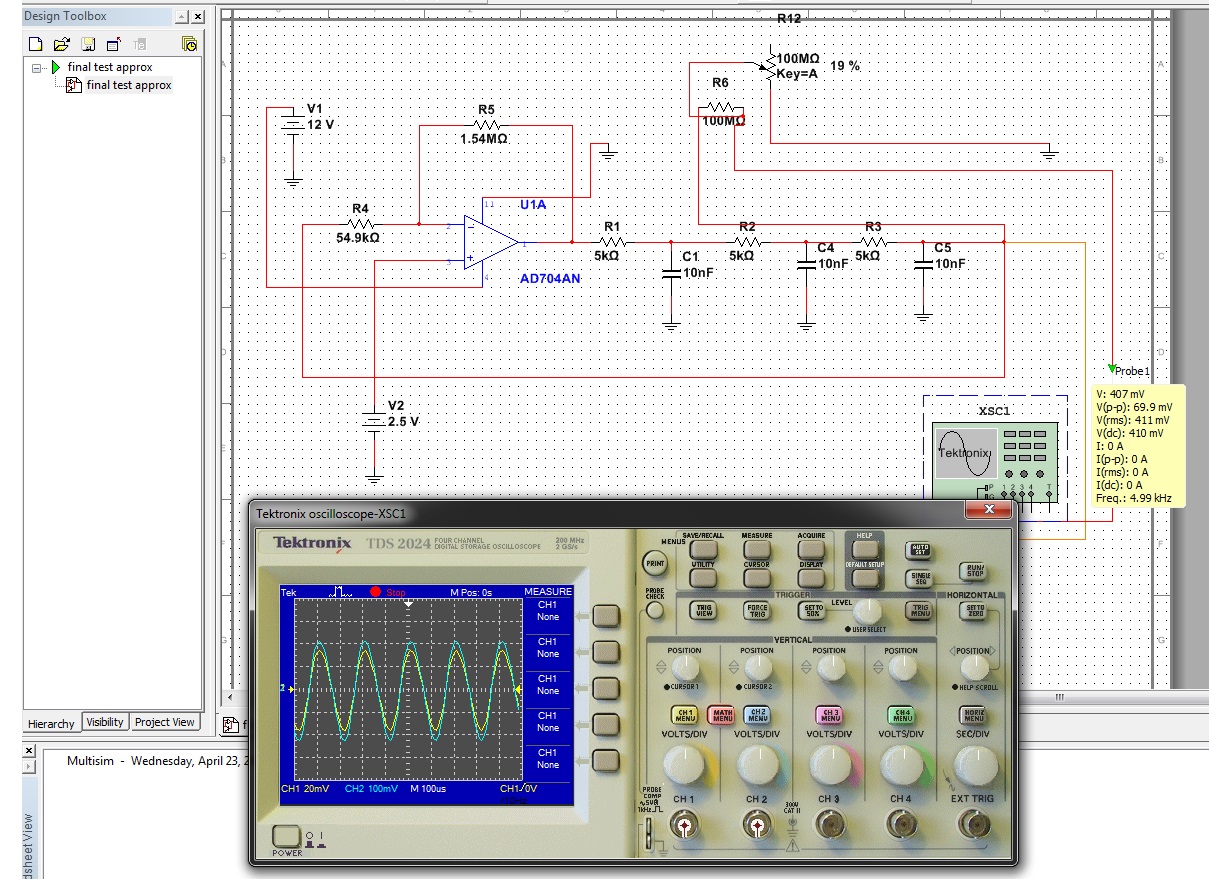
I have read in a book that to determine the frequency, the formula f = (1.732) / (2πRC) is used. it indeed works but I have no idea how to derive this formula. I am kind of new to electronics, could someone help me please? Thanks in advance

 

[Ratch]

Excalibur,



Ratch

 

[Laplace]

According to the Barkhausen stability criterion, the phase shift of the 3-stage RC network must be 180° for oscillation to occur so the phase shift of each RC stage must be 60°. Now it happens that tan(60°)=1.732 so the ratio of the imaginary to the real portion of each RC voltage divider output will equal 1.732 at the oscillation frequency. It takes some complex algebra with imaginary numbers to calculate the RC phase shift. Can you do that?

 

[Ratch]

According to the Barkhausen stability criterion, the phase shift of the 3-stage RC network must be 180° for oscillation to occur so the phase shift of each RC stage must be 60°. Now it happens that tan(60°)=1.732 so the ratio of the imaginary to the real portion of each RC voltage divider output will equal 1.732 at the oscillation frequency. It takes some complex algebra with imaginary numbers to calculate the RC phase shift. Can you do that?

Didn't I already do that above?

Ratch

 

[Excalibur]

Excalibur,

View attachment 12554

Ratch

Using your formula, and the values of capacitor and resistor in the circuit. I get a value for frequency of 7796 Hz
But using the formula of f = (1.732) / (2πRC), I get a value of 5513 Hz. How is that?

 

[Excalibur]

According to the Barkhausen stability criterion, the phase shift of the 3-stage RC network must be 180° for oscillation to occur so the phase shift of each RC stage must be 60°. Now it happens that tan(60°)=1.732 so the ratio of the imaginary to the real portion of each RC voltage divider output will equal 1.732 at the oscillation frequency. It takes some complex algebra with imaginary numbers to calculate the RC phase shift. Can you do that?

Actually, I dont really know how to. Could you please help?

 

[Laplace]

Didn't I already do that above?

Why would you complicate the process for a full 180° phase shift when it is simpler to do it for 60° phase shift?

 

[LvW]

Using your formula, and the values of capacitor and resistor in the circuit. I get a value for frequency of 7796 Hz
But using the formula of f = (1.732) / (2πRC), I get a value of 5513 Hz. How is that?

Exalibur - your formula applies to another phase shift oscillator (1.732=SQRT(3).
More than that - please note that two basic versions of the phase shift oscillator exist:
1.) Three RC lowpass sections: wo=SQRT(6)/RC
2.) Three CR highpass sections: wo=1/[SQRT(6)*RC]

More than that, you should consider that in your circuit R4 loads the last RC section and, therefore, the oscillator frequency will slightly deviate from the ideal.

EDIT: The formula as given by you (factor 1.732) applies to the following phase shift oscillator :
Replace the last RC section and the inverting opamp stage by an active inverting integrator (classical Miller integrator). This has the advantage that the input resistance of the inverter does not load the last RC section.

 

[Excalibur]

Exalibur - your formula applies to another phase shift oscillator (1.732=SQRT(3).
More than that - please note that two basic versions of the phase shift oscillator exist:
1.) Three RC lowpass sections: wo=SQRT(6)/RC
2.) Three CR highpass sections: wo=1/[SQRT(6)*RC]

More than that, you should consider that in your circuit R4 loads the last RC section and, therefore, the oscillator frequency will slightly deviate from the ideal.

A slight deviation would be around 500 Hz. A deviation of 2.7 kHz could be considered a lot. Am i right?

Also, you mentioned that the formula with SQRT(3) is for another phase shift oscillator. Could you be more precise on that one?

 

[LvW]

Also, you mentioned that the formula with SQRT(3) is for another phase shift oscillator. Could you be more precise on that one?

See my last post (EDIT).

 

[Laplace]

See attachment for derivation of formula.

 

[LvW]

See attachment for derivation of formula.

In the attachement you have shown that the phase shift for one single unloaded RC section is 60 deg at a frequency of w=1.732/RC.
Based on this, how can we derive the formula for a series connection of three coupled RC sections (as presented by Ratch) ?

(Comment: Obviously, we cannot assume that each RC sections contributes 60 deg because they are not decoupled. Hence, we must consider the whole network in one single calculation. Your calculation helps only in case we have a circuit with all 3 RC sections decoupled with buffer amplifiers).

 

[Laplace]

The original posting asked how the formula in the book was derived. Do you have a better way to derive that formula?

 

[Ratch]

k

Why would you complicate the process for a full 180° phase shift when it is simpler to do it for 60° phase shift?

Because the 60° single section method relies on the successive section not loading the previous section. My method works no matter what the loading.

Ratch

 

[Ratch]

Using your formula, and the values of capacitor and resistor in the circuit. I get a value for frequency of 7796 Hz
But using the formula of f = (1.732) / (2πRC), I get a value of 5513 Hz. How is that?

Have you tried using a different simulator like the free LTSpice? Did you check out my derivation? The link below gives a similiar formula, but for the R's and C's interchanged.

http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/oscphas.html

Ratch

 

[LvW]

The original posting asked how the formula in the book was derived. Do you have a better way to derive that formula?

Yes - we need the transfer function of the complete 3rd-order RC network and, then, set the imaginary part of the denominator equal to zero. Then, we solve for w.

 

[Arouse1973]

According to the Barkhausen stability criterion, the phase shift of the 3-stage RC network must be 180° for oscillation to occur so the phase shift of each RC stage must be 60°. Now it happens that tan(60°)=1.732 so the ratio of the imaginary to the real portion of each RC voltage divider output will equal 1.732 at the oscillation frequency. It takes some complex algebra with imaginary numbers to calculate the RC phase shift. Can you do that?

Spot on Laplace.
Adam

 

[Ratch]

Spot on Laplace.
Adam

Did you read posts #12 and #14 before making that statement? There are certain conditions that have to be met before you can just add on sections like that.

Ratch

 

[Laplace]

Yes - we need the transfer function of the complete 3rd-order RC network ...

Don't be silly. You will never get the formula in the book that way!

 

[Laplace]

Here is a graph showing the phase shift of third-order RC network calculated two different ways. The Phase.60 (blue) plot shows the phase shift for one RC stage multiplied by a factor of 3. Note that -180° is achieved at a frequency of 5513 Hz, in agreement with the book formula. The Phase.3 (red) plot represents the third-order RC feedback network including the loading of the feedback resistor. Here the -180° point is at 8030 Hz.