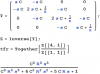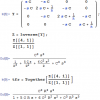Phase shift oscillator help

[Ratch]

View attachment 26639
View attachment 26640

We can proceed like this to find a value of f which makes the imaginary part equal to zero:

View attachment 26641

I looked up some references, and they appear to agree with you that only the transfer function should be used to determine oscillation frequency. It appears that I was wrong about that. Sorry for the confusion.

Ratch

 

[Ratch]

Ratch - sorry, but you are not on the right track in this case.

General (preliminary) remark: If for any oscillator the frequency determining components are given (as in our case) there are still two unknowns to be determined: (1) The oscillation frequency wo and (2) the required gain A of the active deviice. And we have ONE equation to be fulfilled: The oscillation condition which is:
Unity Loop Gain at w=wo; T(jwo)=1.
Hence, we need TWO equations for finding both unknowns.
These two equations are derived from the real and the imaginary part of the loop gain:
Re(T)=1 and Im(T)=0.
Of course, the first equation is identical to R(T)-1=0.
As for each system with two unknowns, both equations (conditions) must be combined (fulfilled) at the same time.
That means: If we find two different expressions for wo from the two equations, both must be equalized to find the final and correct result for wo as well the gain A.



No - the result of both equations [Re(T)=1 and Im(T)=0] as well as all simulations clearly show that the oscillation frequency wo is solely determined by the frequency-determining RC-network (watch the commonly used name of this network!) and not by the amplifiers gain A.
By the way, this is the reason we are allowed to automatically reduce the gain using a non-linear gain determining element (diodes) for rising amplitudes. Otherwise, such an amplitude control would also influence the frequency and the method would be totally "obsolete".

EDIT: Ratch - here is another interesting point which prooves that solving only one of the two equations is not sufficient:

* You have set Im(T)=0 and solved for w. Now - would you expect that inserting your w value into the expression for T would result in a pure real function? This would be the case if your result (last line post#14) is correct.

* However, after inserting your result into T does NOT give a pure real function. The function still is complex with an imaginary numerator and a complex denominator (Re + Im). This clearly indicates that your formula for w in post#14 is not the final solution. Instead, it gives only one of two conditions which must be fulfilled for T(jw) real (Im=0). Hence, we must make use of the second equation which gives A=R2/R=8.

* Only after setting R2=A*R=8R in the denominator gives Re=0 in the denominator and all the "j" (or "i") cancel each other so that the function T(jw) is - as desired - a real function (with T=1 for A=8).
________________________
Sorry for the long answer.
(And I am off for one week now)

See my answer to the Electrician.

Ratch

 

[LvW]

I looked up some references, and they appear to agree with you that only the transfer function should be used to determine oscillation frequency. It appears that I was wrong about that. Sorry for the confusion.
Ratch

May I tell you about an error I have made some time ago?
Somewhere within a relatively long sequence of calculations there was a term SQRT(1E4-1E3) - and I realized that the final result was wrong. But where is the error?
It took me several hours to see that the SQRT was not "1E4/1E3=10" but 9000.
Such things happen from time to time.

 

[LvW]

View attachment 26639
View attachment 26640
.......
We can proceed like this to find a value of f which makes the imaginary part equal to zero:
.............
View attachment 26641

The electrician - I think, what you have done in your relatively long calculation is simply to make use of
Im{T(s)}=Im{H(s)*A}=Im(H(s)=0 (because we can assume that A is fixed and constant value).
The function H(s) is a third-order highpass (three bufferd CR sections).
This is the normal and classical procedure for analysis of all oscillators consisting of a frequency-determining network and a decoupled gain stage.

 

[The Electrician]

The electrician - I think, what you have done in your relatively long calculation is simply to make use of
Im{T(s)}=Im{H(s)*A}=Im(H(s)=0 (because we can assume that A is fixed and constant value).
The function H(s) is a third-order highpass (three bufferd CR sections).
This is the normal and classical procedure for analysis of all oscillators consisting of a frequency-determining network and a decoupled gain stage.

My purpose was to point out that Barkhausen's criterion applies to the loop gain, Aß, not Aß-1.
See: https://en.wikipedia.org/wiki/Barkhausen_stability_criterion

The transfer function referred to in that Wikipedia article is the transfer function only of the feedback network ß. But in this thread Ratch used t(s) to represent the overall loop gain Aß, and not just ß. I used his t(s) in what I posted because he had already established that notation. His t(s) is in fact Aß, which I pointed out in post #57.

Starting from the Barkhausen criterion Aß=1, we must take into account that the criterion has two parts. The magnitude of Aß must be unity; that is, |Aß| = 1, and the angle of Aß must be zero (or a multiple of 360 degrees).

Starting from Aß=1, we just do the usual algebraic manipulation--do the same thing to both sides of the equation, but we have to do the right thing so that we satisfy Barkhausen's criterion.

For the first part, we set |Aß| = |1|.

For the second part, we set angle(Aß) = angle(1), or IM(Aß) = IM(1), which becomes IM(Aß) = 0, where the function IM() means imaginary part. We must not subtract 1 from both sides first, leading to Aß-1 = 0, and then do IM(Aß-1) = 0.

 

[The Electrician]

I was wondering if there was a fast way to derive T(s)?

Like with the buffered one it became easy because once we consider one stage/cube it and then put the gain in there we dont need to use circuit analysis

do you know of a trick for non-buffered RC networks in sequence?

The key is to learn how to set up the problem so a linear algebra solver on your computer is doing all the work:

 

[george2525]

Thanks

Alas I have a phobia of using maths programs and am not good at them.

Also I asked because I have to take tests in these things and am required to solve them by hand. This is extremely annoying.

I understand half of your calculation but what does "tfr = together " mean?

 

[The Electrician]

Thanks

Alas I have a phobia of using maths programs and am not good at them.

Also I asked because I have to take tests in these things and am required to solve them by hand. This is extremely annoying.

I understand half of your calculation but what does "tfr = together " mean?

The "Together" function just puts everything over a common denominator.

Here you can see what the result is before the use of "Together":

 

[LvW]

My purpose was to point out that Barkhausen's criterion applies to the loop gain, Aß, not Aß-1.

Hi Electrician - back from a one-week vacation (with some time to recall our loop gain problem) I like to reply to your contribution as follows:
I think your explanation cannot show why Ratchs derivation could not give the correct results.
At first - the Barkhausen criterion reqires Aß=1, which means (phase condition): Im(Aß)=0.
Rewriting the equation as Aß-1=0 results in the requirement Im(Aß-1)=0 which obviously also will give the correct result regarding the phase.
Hence, both formulations of the criterion can be used.

However, if we perform some mathematical manipulations involving the numerator N(jw) and the denominator D(jw) of the expression ß(jw)=N(jw)/D(jw)=1 we must take into account TWO equations for the real as well as the imag. part (for simplicity I have assumed assumed A=1):
Let´s rewrite the last equation as follows:
N(jw)=D(jw).
In words: The oscillation condition would be fulfilled if the real parts and the imaginary parts of the numerator N(jw) and the denominator D(jw), respectively, are equal [R(N)=R(D) and Im(N)=Im(D)].
The derivation presented by Ratch did take into account the imag. parts only. This is not sufficient - even if the phase condition is considered only.

In the following we can show why the phase condition does not depend on the imag. parts only.
Assuming again A=1 (for simplicity) the complex function of the equation ß(jw)=N(jw)/D(jw)=1 can be separated into a real and a corresponding imag. part.
Because the right side of the equation is real we must set the imag. part equal to zero, which - after some manipulations (multiply conjugate-complex) - gives:
Im(N)*Re(D)-Im(D)*Re(N)=0.
That means: If we analyze the original equation (and do not multiply the basic equation with the complex denominator D) we see that the phase condition involves both imag. and both real parts of the function. Hence, it is not sufficient to equalize the imag. parts only (Im(N)=Im(D), as used by Ratch).

 

[The Electrician]

I was only concerned with Ratch's calculation of the oscillation frequency. He made a mistake in calculating the phase condition which involves setting certain imaginary parts to zero.

I should have been more precise and said that "My purpose was to point out that Barkhausen's criterion applies to the loop gain, Aß, not Aß-1(as calculated by Ratch in post #14)."



Had he done the calculation to set the imaginary parts of Aß to zero, rather than the imaginary parts of Aß-1, he probably wouldn't have made the error because then he couldn't have separated the numerator and denominator of his expression for t as he made the calculation.

 

[LvW]

Had he done the calculation to set the imaginary parts of Aß to zero, rather than the imaginary parts of Aß-1, he probably wouldn't have made the error because then he couldn't have separated the numerator and denominator of his expression for t as he made the calculation.

OK - agreed.