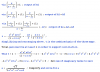Hello,
I am having a lot of trouble understanding the buffered phase shift oscillator below. I think if i can get this one it will help me a lot with others. The first figure shows the standard positive FB block diagram and its formula. I get this.
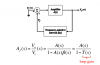
I can also accept that the shown value for B under the oscillator figure is correct. I understand that this is the portion of Vo fed back to the inverting amplifier input terminal (at V3)
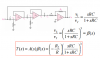
but then it is implied that A = -R2/R which is causing me the trouble. Why is A (open loop gain) the closed loop gain of the ideal inverting amplifier? and not A3?
I realise that R2 is also providing feedback here but then shouldn't this also be incorporated into the value for B and not into the value for A?
Looking at the first figure (block diagram) it seems to me that Vo/Vi = A/(1-AB) ....ok so why is Vo/Vi = AB = "T(s)" in the oscillator figure!?
Can anyone clear this up for me?
or answer the following please!
1. what is the standard formula for B (feedback) here?
2. what is the gain labelled "Af" in the block diagram as applied to the oscillator?
3. What is A here and why is it -R2/R and not simply A3 (third op amp intrinsic gain)?
Thanks, any help would be great!
I am having a lot of trouble understanding the buffered phase shift oscillator below. I think if i can get this one it will help me a lot with others. The first figure shows the standard positive FB block diagram and its formula. I get this.
I can also accept that the shown value for B under the oscillator figure is correct. I understand that this is the portion of Vo fed back to the inverting amplifier input terminal (at V3)
but then it is implied that A = -R2/R which is causing me the trouble. Why is A (open loop gain) the closed loop gain of the ideal inverting amplifier? and not A3?
I realise that R2 is also providing feedback here but then shouldn't this also be incorporated into the value for B and not into the value for A?
Looking at the first figure (block diagram) it seems to me that Vo/Vi = A/(1-AB) ....ok so why is Vo/Vi = AB = "T(s)" in the oscillator figure!?
Can anyone clear this up for me?
or answer the following please!
1. what is the standard formula for B (feedback) here?
2. what is the gain labelled "Af" in the block diagram as applied to the oscillator?
3. What is A here and why is it -R2/R and not simply A3 (third op amp intrinsic gain)?
Thanks, any help would be great!