Yes, in simple i want to measure a continuously varying signal using MAX1204. say a sine wave of 1.2V peak to peak.
*"You need to superimpose the sinewave on a DC bias voltage" -> what does this mean ?
what additional changes i need to change in MAX1204 circuit to measure a sine wave ?
This is a simple and common way to do it:
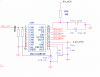
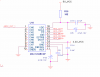
The resistors must be of equal value. They divide the reference voltage in half and set the ADC input voltage so it's centered around that voltage. So when no signal is present, the ADC should read half-scale. The resistors should be 1% or better. The signal is coupled onto the ADC input by the capacitor, which should be chosen so its reactance is very much lower than the impedance of the voltage divider at the lowest frequency of interest.
For example, common values would be 100k for each resistor, and 1 µF for the capacitor. Aiming for X
C < Z
DIVIDER / 10, you need to ensure that X
C < 5 kΩ. This is true down to a frequency of F = 1 / (2 pi C X
C)
= 1 / (2 × 3.14 × 1 × 10
-6 × 5000)
= 32 Hz.
So with 2x 100 kΩ and 1 µF, frequencies down to about 32 Hz will be reproduced pretty accurately.
Say i am measuring a 1.2Vpp sine wave. and I want to get a continuous stream of digital values correspond to. 1.2V,1V,0.5V. The ADC may measure 1.2V at a time but next i want to get the 1V. but ADC samples say 0.75V or it may sample another random value. How can we avoid such randomness ?
Well, you need to sample at several times the highest frequency in the input signal. You mentioned a 1 kHz sinewave. The Nyquist frequency, which is twice the highest frequency in the input signal, i.e. 2000 samples per second for this example, is sometimes considered the minimum sampling rate that you need, but sampling at that frequency won't show you the proper shape of the waveform though. The faster you sample, the more accurately you will capture the shape of the waveform.