Is there an equation I can use to find DV/DT?
If you have V in terms of t you can. Something like this maybe:
V=sin (t)
Is there an equation I can use to find DV/DT?
I already have the 5Vrms given to me for V.
Resistance by definition is the ratio of voltage to current (period!).
It's units are therefore Volts/Amp. Resistors are devices whose voltage is
proportional to the current over a wide range of currents.
Capacitors are only a tiny bit more complicated.
Capacitance is the ratio of current to the "change in voltage over time".
In reality there is a trick which actually makes the problem much simpler.
Engineers use radians.
Nevertheless, for dQ/dt = I the "I" would be physically measured as current flowing through the capacitor.... Differentiating both sides with respect to t gives dQ/dt = I = C dV/t ... Keep in mind that that no charge passes through the dielectric of the cap.;
LOL. Never go into teaching.I agree. As an aside, V/I is not Ohm's law. We can discuss that later.
I disagree. Caps are a lot more complicated because they store energy while resistors do not. Resistors reduce current because they dissipate electrical energy. Caps reduce current because they produce a back voltage. Each reduces current by entirely different methods.
The basic definition of capacitance is the amount of charge that can be deposited on one plate of the cap per volt of difference between plates, C = Q/V . Capacity is the ability of the capacitor to store energy and change charge on both plates. As V increases, so does Q. This means that C will be constant for a given cap.
No tricks involved. Direct calculation is all that is needed. Recall Q = C V. Differentiating both sides with respect to t gives dQ/dt = I = C dV/t = C d(5 sqrt(2) sin(w t))/dt = C w 5 sqrt(2) cos(w t) = 0.47E-6 2 pi 100 5 sqrt(2) cos(2 pi 100) = 2.09 E-3 cos(628.32t) . So I = 2.09E-3 cos(628.32 t) , where 628.32 is radians/sec . Keep in mind that that no charge passes through the dielectric of the cap.;
Differential and integral calculus uses radians.
Ratch
Nevertheless, for dQ/dt = I the "I" would be physically measured as current flowing through the capacitor.
LOL. Never go into teaching.
Do you really mean charge flowing through the cap? Doesn't happen. If it did, the cap would be leaky and defective. What you will observe is the charge accumulating and depleting on the plates of the cap. That is much different than current existing through the cap. I thought we settled that earlier. What is it about flow of charge you don't understand?
Perhaps this thought will help. If current existed through the cap, charge would not accumulate and deplete on its plates, and the cap could not be energized to a voltage. Just like a resistor cannot be energized.
Ratch
Didn't I sufficiently explain what I meant? Perhaps a diagram will provide clarification. The current 'I' in the equation I=C⋅dV/dt is measured as the current flowing through the capacitor. Would there be any other possible way to measure 'I'?Do you really mean charge flowing through the cap?
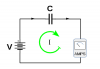
What do you think?What is it about flow of charge you don't understand?
="Electrical Engineer David, post: 1733345, member: 48873"]
Do you honestly think I didn't know that already. In fact I think not only did I realize this, I suspect he did as well. Are you just trying to spout out all you know in an effort to confuse or perhaps bolster your ego? Teaching is about understanding where your students are and taking them to the next step. Not proving to them how much you know and in the process only serve to confuse matters more for them. It's immaterial to the point and doesn't serve to clarify his question.
Not one of your "clarifications" to me wasn't previously understood by myself and not one served to promote his understanding. Leave out the superfluous until they understand the big picture, "What does the equation mean and how do you use it?". How would pointing out that current (I) is equal to dQ/dt resulting in dQ/dt divided by dV/dt resulting in dQ/dV have provided clarification to someone who is just learning what rms means let alone a solid foundation in differential calculus? Are you trying to frustrate them and drive them off from what is a fascinating and, yes, easy to understand science? Should we tell them capacitors are very complicated and not easily understood then confuse them just to prove it? His equation was in the form of either C = Ic / dV/dt or Ic = C * dV/dt
By the way, I considered starting with C=Q/V then deriving his equation and rejected it, knowing he hadn't had DE and perhaps not even Trigonometry. Also why I didn't correct my subtle miss statement about the slope of sine being 1 at the origin. It isn't, its equal to 2*pi*amplitude = 6.28 for a 1 Hz signal because the sine source is actually sin(2*pi*t). Think that would have helped him too? If he had recognized this only then would I have tried to clarify.
Didn't I sufficiently explain what I meant? Perhaps a diagram will provide clarification. The current 'I' in the equation I=C⋅dV/dt is measured as the current flowing through the capacitor. Would there be any other possible way to measure 'I'?
View attachment 34319
What do you think?
And that would be wrong. One needs to think of this in terms of a complete circuit. The current being measured is the 'I' circulating in the loop. Maxwell provided a correction to Ampere's Law in order to explain why this is so; but that is more complicated than is necessary to understand how a capacitor behaves in a circuit. Nothing more is necessary for circuit analysis than the differential equation relating the capacitor voltage to the current flowing through the capacitor.I think you are measuring the charge flow released by the dielectric next to the right plate of the capacitor.
And that would be wrong. One needs to think of this in terms of a complete circuit. The current being measured is the 'I' circulating in the loop. Maxwell provided a correction to Ampere's Law in order to explain why this is so; but that is more complicated than is necessary to understand how a capacitor behaves in a circuit. Nothing more is necessary for circuit analysis than the differential equation relating the capacitor voltage to the current flowing through the capacitor.
You seem to misunderstand the situation here. I am trying to help YOU understand how we do circuit analysis with capacitors.I have exhausted my ability to explain the operation of a capacitor to you.
You seem to misunderstand the situation here. I am trying to help YOU understand how we do circuit analysis with capacitors.
My apologies. I misunderstood to whom it was directed.You are confused. Look at post #30 of this thread and observe to whom my reply was addressed. It certainly was not to you. I do assume you know that charge does not flow through the dielectric of a cap, but Laplace doesn't seem to understand that. He has challenged me several times about this point in this and past threads.
I do not consider myself a teacher or those who ask questions in this thread my students. I am more of a knowledge base who may impart some knowledge to those who ask.
In you reply above, you refer to "he" and "his question". To whom does the pronoun refer, Laplace or the OP?
The OP asked where to find dv and dt. I gave him a succinct answer, not a rambling dialog or a DE course. It must have answered his question because I did see any follow up. By the way, surely you must agree that caps are more than a tiny bit more complicated than resistors. Telling someone otherwise does not help them.
If you ask ten different people the OP's question, you would probably get ten different answers. The OP has to decide which answer his likes best.
Ratch
