hevans1944
Hop - AC8NS
If you can resolve two (and only two) distinct peaks with the spectrum analyzer, I assume you are connecting the spectrum analyzer input to the summed waveforms, f1 and f2, which are used as references for the two lock-ins.
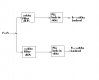
It should be possible to separate these, with band-pass filters, for control of two separate phase-locked f1 /4 and f2 /4 oscillators. The band-pass filters would be tuned to 150 kHz and 160 kHz and each should have about 1 kHz bandwidth at the -3 dB roll-off skirts so there would be about 8 kHz separation in their frequency response.
The sinusoidal outputs of the two filters need to be passed through Schmitt triggers to create fast square-wave edges to apply to two two-stage binary dividers whose outputs are f1 /4 and f2 /4. The binary divider outputs are used to phase-lock two variable frequency voltage-controlled oscillators running at f1 /4 and f2 /4 and outputting triangle waveforms. The triangle-wave outputs are then applied to a piece-wise linear diode wave-shaping circuit to produce sine waves at f1 /4 and f2 /4 frequencies. Using a linear analog op-amp you can now sum these two frequencies and apply them as excitation to your cantilever.
Theoretically, you could just pass the f1 /4 and f2 /4 square waves from the binary dividers through two band-pass filters to remove the harmonic content of the square waves. This may work, but it destroys the phase coherence of the divided waveforms with respect to the original higher frequency f1 and f2 sinusoids. Phase-locking a VFO to these divided waveforms preserves the phase coherence, as does subsequent analog processing by the piece-wise linear diode circuitry. I can't say whether preserving the phase coherence is important or not because I don't know how your touching contact extracts information from the probe.
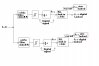
I don't have any recent practical experience constructing narrow-band filters, so if you have an electronics lab with a skilled technician or electrical engineer available, that would help to eliminate any false starts. The first thing I would do is breadboard two Sallen-Key 2nd-order bandpass filters, each with a Q=10 and center frequencies of 150 kHz and 160 kHz. Apply your summed f1 and f2 outputs to the inputs of these filters and check their outputs with your spectrum analyzer. We would like to see negligible 160 kHz output from the 150 kHz filter, and likewise negligible 150 kHz output from the 160 kHz filter. Assuming you get more-or-less single frequency sine waves at the output of the two filter, pass those waveforms to Schmitt triggers to convert the sine waves to square waves.
If all has gone well up to this point, pass the square waves as clock signals to two pairs of D-type flip-flops connected to provide an output divided by four. Then build two more bandpass filters like the first two but with center frequencies of f1 /4 and f2 /4 and pass the square waves into them. A sinusoidal output should result, but its phase will be indeterminate with respect to f1 and f2. Try summing these two signals anyway, and driving the cantilever to see if you get the results you expect.
If not, then the f1 /4 and f2 /4 square waves will have to used as references to phase-lock a VCO (voltage-controlled oscillator) and since the VCO doesn't generate sine waves, more circuitry will be required to make a sinusoidal output. A suitable integrated circuit to implement a phase-locked oscillator is the Texas Instruments CD4046B. Application note here. Square waves from its internal VCO can be integrated with analog circuits to provide triangle waves, and those can be passed into a piece-wise linear break-point attenuator to make sine waves. There is a plethora of circuits available to do this.
Well, I hope I have given you some ideas to try out. This sounds like a "fun" project and I wish I could be there to help you. So, if my above description doesn't sound like something out of left field, please let me know what you think.
Ions? You are dipping your probe into a liquid?
It should be possible to separate these, with band-pass filters, for control of two separate phase-locked f1 /4 and f2 /4 oscillators. The band-pass filters would be tuned to 150 kHz and 160 kHz and each should have about 1 kHz bandwidth at the -3 dB roll-off skirts so there would be about 8 kHz separation in their frequency response.
The sinusoidal outputs of the two filters need to be passed through Schmitt triggers to create fast square-wave edges to apply to two two-stage binary dividers whose outputs are f1 /4 and f2 /4. The binary divider outputs are used to phase-lock two variable frequency voltage-controlled oscillators running at f1 /4 and f2 /4 and outputting triangle waveforms. The triangle-wave outputs are then applied to a piece-wise linear diode wave-shaping circuit to produce sine waves at f1 /4 and f2 /4 frequencies. Using a linear analog op-amp you can now sum these two frequencies and apply them as excitation to your cantilever.
Theoretically, you could just pass the f1 /4 and f2 /4 square waves from the binary dividers through two band-pass filters to remove the harmonic content of the square waves. This may work, but it destroys the phase coherence of the divided waveforms with respect to the original higher frequency f1 and f2 sinusoids. Phase-locking a VFO to these divided waveforms preserves the phase coherence, as does subsequent analog processing by the piece-wise linear diode circuitry. I can't say whether preserving the phase coherence is important or not because I don't know how your touching contact extracts information from the probe.
I don't have any recent practical experience constructing narrow-band filters, so if you have an electronics lab with a skilled technician or electrical engineer available, that would help to eliminate any false starts. The first thing I would do is breadboard two Sallen-Key 2nd-order bandpass filters, each with a Q=10 and center frequencies of 150 kHz and 160 kHz. Apply your summed f1 and f2 outputs to the inputs of these filters and check their outputs with your spectrum analyzer. We would like to see negligible 160 kHz output from the 150 kHz filter, and likewise negligible 150 kHz output from the 160 kHz filter. Assuming you get more-or-less single frequency sine waves at the output of the two filter, pass those waveforms to Schmitt triggers to convert the sine waves to square waves.
If all has gone well up to this point, pass the square waves as clock signals to two pairs of D-type flip-flops connected to provide an output divided by four. Then build two more bandpass filters like the first two but with center frequencies of f1 /4 and f2 /4 and pass the square waves into them. A sinusoidal output should result, but its phase will be indeterminate with respect to f1 and f2. Try summing these two signals anyway, and driving the cantilever to see if you get the results you expect.
If not, then the f1 /4 and f2 /4 square waves will have to used as references to phase-lock a VCO (voltage-controlled oscillator) and since the VCO doesn't generate sine waves, more circuitry will be required to make a sinusoidal output. A suitable integrated circuit to implement a phase-locked oscillator is the Texas Instruments CD4046B. Application note here. Square waves from its internal VCO can be integrated with analog circuits to provide triangle waves, and those can be passed into a piece-wise linear break-point attenuator to make sine waves. There is a plethora of circuits available to do this.
Well, I hope I have given you some ideas to try out. This sounds like a "fun" project and I wish I could be there to help you. So, if my above description doesn't sound like something out of left field, please let me know what you think.
Ions? You are dipping your probe into a liquid?