I'm afraid there are some problems with this approach because of the electrical characteristics of the solar panels.
An array of solar panels is a voltage source; the amount of voltage it generates depends mainly on two factors: the amount of sunlight, and the amount of current that's being drawn from it. I'm going to assume there will be a constant amount of sunlight falling on the solar array. In this case, the voltage decreases as you draw more current from it, as shown by the following graph.
(The graph is from
http://www.mtmscientific.com/solarpanel.html.)
The voltage will be at maximum when no current is being drawn from the solar array; this is the unloaded state. As you start to draw more and more current from it, the voltage will drop fairly smoothly until the "knee" of the curve is reached, and the voltage starts to drop off quite quickly as the load current is increased. At the end of the curve, there's no voltage left; this is the short circuit current that davenn mentioned in post #2.
There is a point on the knee called the "maximum power point" which I will describe later. At the moment, just see how the voltage behaves depending on the amount of current drawn from it.
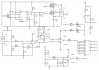
When charging is active, your circuit simply connects the solar panel directly to the battery via the two MOSFETs. The MOSFETs do have a certain ON-resistance, Rds(on), but it's pretty small and can be pretty much ignored. Say the battery is charged to 1.2V, and the solar array's unloaded voltage is around 2V. Because of this voltage difference, current will flow. The solar panel will try to pull the battery's voltage up to 2V, but the battery will not allow this. Current will flow from the solar array to the battery. They will play a tug-of-war game, with the current being represented by the tension in the rope. The voltage will stabilise somewhere, probably around 1.4V or so, because the battery is more "stubborn" than the solar array - the internal resistance of a charged battery is lower than that of a solar panel, especially a small one.
The amount of current that the solar array can supply depends on the voltage, according to that graph. It also depends very much on the amount of sunlight falling on the solar array, which is a separate factor that is not shown on the graph and which I've assumed to be constant so far. The result is that the amount of current that flows from the solar array to the battery will be almost completely dependent on the amount of sunlight falling on it. This will also affect the voltage to a lesser extent.
There is no explicit current limiting in this arrangement. The small ON-resistance of the MOSFETs is not a significant factor here. You would be relying on the solar array's own electrical characteristics to limit the current, and the current that the solar array can produce depends on the amount of sunlight falling on it.
To start with, this means that the rate of charge for the battery will vary constantly as the sunlight varies. The only way that I know of to work around this problem is to have a huge solar array that can deliver the required amount of voltage and current even at low sunlight, then waste most of its capacity most of the time. I'm going to assume that's not a workable option for you.
The next problem is detecting the charge termination condition. With the charging current varying over a fairly wide range, it becomes impossible to reliably detect charge termination. The "negative delta V" method, aka peak voltage, won't work, because the voltage will be rising and falling with the sunlight level; as soon as a cloud blocks some of the sunlight, the voltage will drop, and the falling voltage detector will terminate the charge. In any case, the negative delta V condition is only a reliable indication of full charge when an NiMH battery is being charged at a current of 0.5C or higher.
End-of-charge detection via rate of temperature rise will also be unreliable if the charging current is varying widely, because the battery will cool down during low current periods and could end up being overcharged because the target temperature gradient never occurs within the expected time period.
A few other comments on your design.
I suggest you note that U4 is attached to the battery. This can be inferred but I think it should be stated clearly.
You only need one MOSFET in series with the battery; you should combine the two Stop conditions into a single signal to control that MOSFET. Otherwise you waste a bit of energy in the extra MOSFET, and a bit of money too. But this is irrelevant because that approach isn't going to work anyway.
I don't know whether you need to prevent the battery from back-feeding in to the solar array. See whether the solar panel data sheet says anything about it. If you do, you'll need another MOSFET in series, but with the opposite orientation, so that its body diode will not be forward-biased in that situation.
Edit: Oops I forgot to get back to the maximum power point. This is the point on the curve in the graph where the power available from the panel is the highest. Power is voltage multiplied by current. Solar-powered equipment, especially large equipment where maximum power is very important and circuit complexity and cost is less important, can detect and track the maximum power point in real time, to ensure that maximum energy is always extracted from the available sunlight.