Trying to get back back into this. been away for a very long time. Taking a course on the fundamentals of basic electronics.
Here is what I need help with:
The following circuit depicts a blocking oscillator during the initial instant after triggering. By means of Kirchhoff’s Voltages Law, find the currents flowing in the branches containing the 93.6 and 164 volt batteries. Also calculate the value of ec.
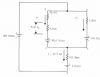
Here is what I need help with:
The following circuit depicts a blocking oscillator during the initial instant after triggering. By means of Kirchhoff’s Voltages Law, find the currents flowing in the branches containing the 93.6 and 164 volt batteries. Also calculate the value of ec.

