Low frequency FET response, determining f[sub]L[/sub] of Cs capacitor

[nvjnj]

I'm trying to get the low frequency cutoff value of the capacitor Cs of the following ac equivalent circuit using the equation:
f(L)=1/(2*pi*Req*Cs)

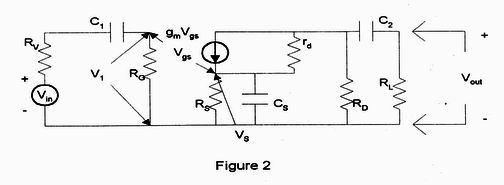
To do this, I'm supposed to reduce the circuit "seen" by capacitor Cs to an equivalent RC circuit where Req would be the equivalent resistance seen by Cs.

Employing Thevenin's Theorem, open-circuiting all current sources and short circuiting all voltage sources gives me the equivalent resistance as:

Req=R_S||((R_L||R_D)+r_d) which simpifies into the equation:
Req=R_S/(1+(R_S/(R_DR_L+r_d)))

But the real equation stated in the internet and text books is:
Req=R_S/(1+(R_S(1+g_mr_d)/(R_DR_L+r_d)))

So, I am missing the factor (1+g_mr_d) in my equation. Please help me figure out what I am doing wrong.

 

[(*steve*)]

there is a current source there which is a dependent current source. You can't just open circuit that.

 

[nvjnj]

there is a current source there which is a dependent current source. You can't just open circuit that.

I see....I missed that.
Thanks....I'll try to redo it

 

[nvjnj]

I see....I missed that.
Thanks....I'll try to redo it

Okay, so I tried doing it by not removing the dependent current source. But I'm still not getting the answer. These are the steps I followed:

Req=V(open-circuit)/I(short-circuit)

V(open-circuit):
Open circuiting Cs, Voltage across this open circuit is equal to voltage across Rs. Voltage across Rs = Is*Rs, where Is is the current flowing through Rs.
Is=(r_d/(r_d+(R_s+R_D||R_L)))*g_mV_gs

Therefore V(short-circuit)=(r_d*Rs/(r_d+(R_s+R_D||R_L)))*g_mV_gs

I(short-circuit):
Short circuiting Cs would make Rs redundant and is removed. Hence current accross this path is:
Is=(r_d/(r_d+(R_D||R_L)))*g_mV_gs

Hence Req=(r_d*Rs/(r_d+(R_s+R_D||R_L)))*g_mV_gs / (r_d/(r_d+(R_D||R_L)))*g_mV_gs

This eliminates my g_m terms, which is required in the final equation as stated in the original post. Please tell me what I am doing wrong?

 

[(*steve*)]

Why did you calculate V(short circuit)?

 

[nvjnj]

Why did you calculate V(short circuit)?

Sorry, that was a typo, its actually V(open-circuit)=(rd*Rs/(rd+(Rs+RD||RL)))*gmVgs

 

[Laplace]

Following online book has a clue on how to find the equivalent resistance:
https://books.google.com/books?id=q...VvTR&dq=cutoff=bl&pg=PA182#v=onepage&q&f=true