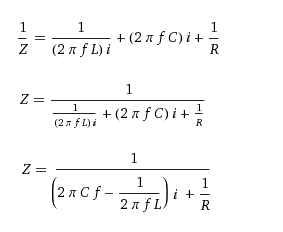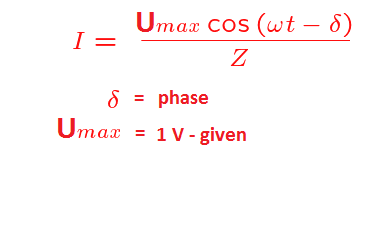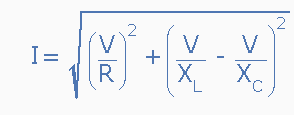LC circuit tasks

[evol_w10lv]

I have also got LC circuit task.
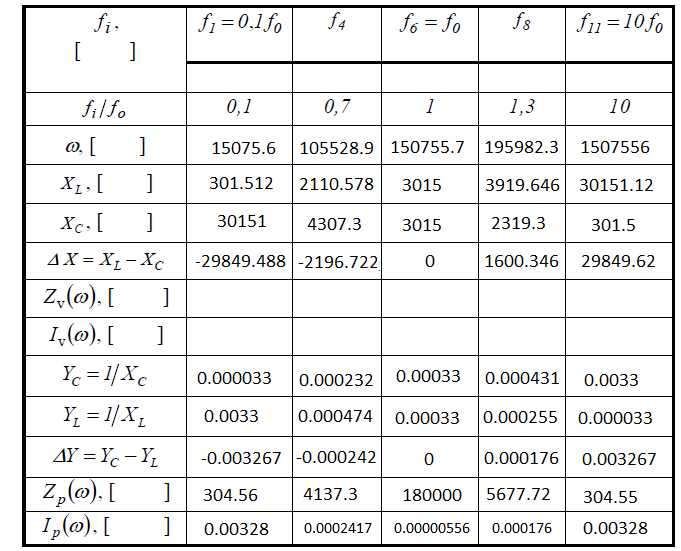
I add table, where are values, which I have to calculate (I guess all denotations/symbols are international):

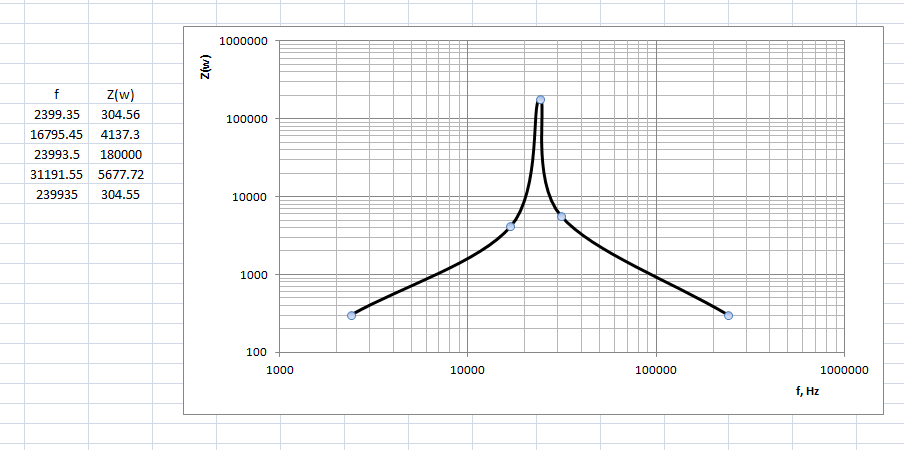
1.1 We have got parallel LC circuit.

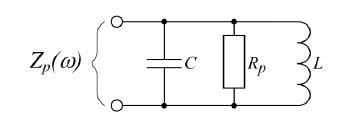
Have to calculate frequency f0, ratio of charge Q and total impedance Z(w) in the range (0.1 .. 10)f0.
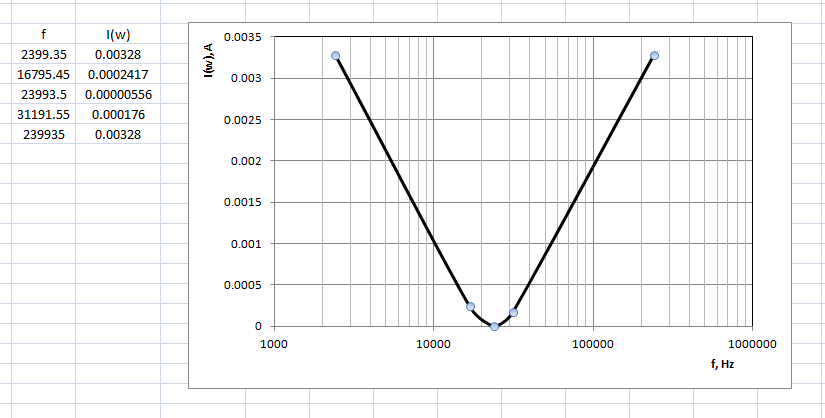
And have to calculate input current (effective value) using given frequencies in the table, if we know that is added sinusoidal voltage amplitude 1 V to the circuit.

1.2 We have got series LC circuit.

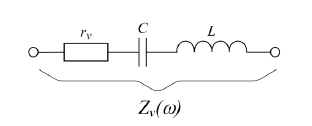
GIVEN:
Rp = 180 kOhms = 180 * 10^3 Ohms
C = 2200 pF = 2200 * 10^(-12) F
L = 20 mH = 20 * 10^(-3) H


What I have already done:
I calculated frequency f0 for parallel and series circuits: w0 = 2*pi*f0 = 1/sqrt(L*C)
w0 = 1/sqrt(20*10^(-3) * 2200*10^(-12)) = 500000/sqrt(11) = ~150755.7
f0 = w0/(2pi) = (500000/sqrt(11))/2pi = 250000/(sqrt(11)*pi) = ~23993.5 Hz
XL = XC
XL = w * L = (500000/sqrt(11)) * 20*10^(-3) = 10000/sqrt(11) = ~3015
XC = 1/(w*C) = 1/((500000/sqrt(11))*2200*10^(-12)) = 10000/sqrt(11) = ~3015
for parallel circuit: Q = Rp/(w0*L) = 180*10^3/((500000/sqrt(11))*20*10^(-3)) = 18 sqrt(11) = ~60
Yc = 1/Xc = 1/(10000/sqrt(11)) = sqrt(11)/10000 = ~ 0.00033
YL = 1/XL = 1/(10000/sqrt(11)) = sqrt(11)/10000 = ~ 0.00033

I have got lack of understanding, why I have to calculate delta Y and delta X? Or I have done something wrong? XL = XC and YC = YL.. where is the point?
And speaking about parallel circuit, how to do this task - calculate input current (effective value) using given frequencies in the table, if we know that is added sinusoidal voltage amplitude 1 V to the circuit?
Later I will start to solve other tasks with series circuit, but yes, can someone can explain my questions..

 

[Harald Kapp]

why I have to calculate delta Y and delta X?

Well, primarily because your instructor wants you to do so. It's not always useful to question the intentions of the instructor.
Second, because you will note something interesting if you look at these differences for different frequencies.

calculate input current (effective value) using given frequencies in the table, if we know that is added sinusoidal voltage amplitude 1 V to the circuit?

For this you have to calculate the complex impedance of the parallel circuit. No use looking at the individual impedances of L and C because at f0 the circuit becomes resonant. Once you have the complex impedance Z(L,C,f) as a function of L, C and the frequency, you can apply Ohm's law and calculate I=U/Z where all variables are complex (meaning they have amplitude as well as phase). Hint: at f=f0 the impedances of L and C have the same magitude, but are 80° out of phase.

See here for some more informative text.

 

[evol_w10lv]

Yes, I get it why do we need delta delta Y and delta X. XL and XC changes at different frequencies (as you mentioned). It was awkward question.

But I still don't really understand, how to get input current.
I guess, this is complex impedance Z(L,C,f):

But how to get complex U without depending on time?
Is there is no other way, how to calculate current without complex variables? We can calculate Z at any different frequencies, is there no way to calculate U at different frequencies?
When I get this, I actuallu don't know, how to continue the task:

Maybe you can give me an example, how to calculate current with your suggested method..

 

[Harald Kapp]

But how to get complex U without depending on time?

Wrong start. You apply U and get I - because U=1V i given.

Your second image shows that you are on the right track with this, but you are not yet there. Forget about the concrete definition of U=Umax*cos(wt-delta). Simply set U=U(t). This may be awkward to you since you think of U as a sinusoidal signal (which ist is), but that detail is not necessary here.
For any U you have I=U/Z. Since Z is a complex impedance, the resulting current will be complex, too. Which means it will have a form I=f(U,f). And since in the equation for Z there is no cos() or sin(), you wil find that the expression for I=f(U,f) has no sin() or cos() either. You will be able to represent I as I=Ireal+i*Iimag.
Now observe what happens if you make f->f0. You can fill in the table provided to you or graph the function I=f(f) if you set U=1V (just for ease of computation).

Study this tutorial or Google for lc circuit analysis

 

[evol_w10lv]

Great tutorial. It will help for me not just for this task.

I used this formula:

I calculated 5 values. Yes, it is not enough to get perfect graphic, but here is result:

All calculations I did by this algorithm:
f1:
f0 = ~23993.5 Hz
f1 = 0.1f0 = 2399.35 Hz
w = 2*pi*f1 = 2*pi*2399.35 = ~15075.6
XL = w * L = 15075.6 * 20*10^(-3) = 301.512
XC = 1/(w*C) = 1/(15075.6*2200*10^(-12)) = ~30151
delta X = XL - XC = 301.512 - 30151 = -29849.488
Yc = 1/Xc = 1/30151 = ~0.000033
YL = 1/XL = 1/301.512 = 0.0033
deltaY = YC - YL = 0.000033 - 0.0033 = -0.003267
Z = 1/(sqrt((1/R)^2 + ((1/XL)-(1/XC))^2)) = 1/(sqrt((1/180000)^2 + ((1/301.512)-(1/30151))^2)) = ~304.56
I = sqrt((U/R)^2 + ((U/XL)-(U/XC))^2) = sqrt((1/180000)^2 + ((1/301.512)-(1/30151))^2) = ~0.00328 A

Then I started to complete the table:

Can you take a look? I'm not speaking about results, but I want to know, weather content/essence is clear. And free spaces in the table left for series circuit. I will solve it later.

 

[Harald Kapp]

I don't have time to check the numbers in the table. But the graphics look exactly like I would have expected.

Good work.

 

[evol_w10lv]

To calculate impedance Z without rv it is Z = sqrt((Xl-Xc)^2)?