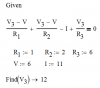I wouldn't worry too much about that

The beauty of these courses is that you can do them multiple times at the same cost ($0). The other thing to remember is that this course is a *real* engineering unit. It's not fluff put out on the internet to give people entertainment. Learn what you can. Move through the weeks at your own pace and try to become proficient. Being able to understand this stuff is more important than being able to get the right answers one time on a test.
As I was doing this stuff there were times that I had to sit and think for quite some time to do the problem in the way they wanted it done. In many cases I could almost solve the problem by inspection (knowing many shortcuts from years of experience) but I had never done this using the basic laws.
Several pointers:
1) Take notes during the lectures and keep them by your side.
2) have another book of rules and identities for various solved problems which look significant. For example the equation for a voltage divider, or resistors in parallel. Have you covered conductance vs resistance yet? Converting from one to the other can make some things far easier.
3) Dilligently do all the exercises, not just the assessed ones.
4) Find some web sites which can find symbolic answers to equations. Later on, you'll find the equations you generate are *horrible* and solving them is a PITA These will help with the mechanical work. (I have some of these bookmarked on another computer. I'll try to remember to post the links later.)
5) make sure you understand how the MIT software handles formula input. It can be dicky and the last thing you want is to use up your three tries just getting the right answer into a format the software understands.
6) Use the forums in the MIT software. I found them to be somewhat useful. They were very useful when I did this course, but were buggerized about for other courses which made them much harder to use. Beware that people do occasionally post the complete method for answering a question. Great for getting the right answer, not so great to learn from.
When you come to the exams in this course, beware that they are as hard as any exam I have done. They have questions that range from easy to really hard -- they are designed to produce a result which distinguishes skilled from non-skilled people, NOT to allow everyone to pass. The points in steps 1 and 2 above will be a great help.