Hello everyone, this is my first time posting in this forum.
I have basically zero experience calculating circuits on my own, usualy, I just do the manual labor (soldering, etc)
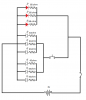
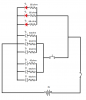
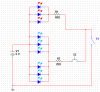
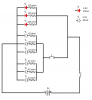
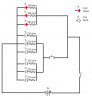
My current client needs the following circuit in his product, and I'm having trouble calculating the resistance of the resistors.
The circuit is pretty simple, it's three groups of LEDs (two white, and one red), with a power switch, and a momentary button for the white LEDs.
Space is limited, so I can only fit some 3V coin cells, or two AAA batteries inside. The red LEDs need 2.2V and 20mA, and the white ones need 3.5V and 20mA.
So, if I power it using two AAA batteries will it work properly? The white LEDs will be a little bit weak, since I'll get 3V maximum. Or should I go for a couple of 3V cells? It will get me 6V and require less space than the batteries.
And what's the math I need to do to know the resistance of the resistors? I found some online calculators, but they only calculate on the ideia that all the LEDs are equal. Since I'm using two different types of LEDs, I'm can't find the answer.
Can someone give me the formula?
PS: Is it an option to use the AAA bateries and connect the white LEDs whitout resistors? The voltage will do, but I fear the current will damage the LEDs.
Thanks in advance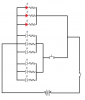
I have basically zero experience calculating circuits on my own, usualy, I just do the manual labor (soldering, etc)
My current client needs the following circuit in his product, and I'm having trouble calculating the resistance of the resistors.
The circuit is pretty simple, it's three groups of LEDs (two white, and one red), with a power switch, and a momentary button for the white LEDs.
Space is limited, so I can only fit some 3V coin cells, or two AAA batteries inside. The red LEDs need 2.2V and 20mA, and the white ones need 3.5V and 20mA.
So, if I power it using two AAA batteries will it work properly? The white LEDs will be a little bit weak, since I'll get 3V maximum. Or should I go for a couple of 3V cells? It will get me 6V and require less space than the batteries.
And what's the math I need to do to know the resistance of the resistors? I found some online calculators, but they only calculate on the ideia that all the LEDs are equal. Since I'm using two different types of LEDs, I'm can't find the answer.
Can someone give me the formula?
PS: Is it an option to use the AAA bateries and connect the white LEDs whitout resistors? The voltage will do, but I fear the current will damage the LEDs.
Thanks in advance