Gate Charging App Note Problem

[BlackMelon]

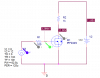
Hello,

I read the Microchip's app note in the attached files, making me curious about the gate current equation. (I understand the idea of charging cap but this look too simple). So, I made a simple switching simulation below. The input is 5-0V pulse having 10ns of rise and fall time. I measured the current waveform through R1: I(R1).
To see if the equation highlighted in the app note is valid or not, I calculated the average value of I(R1) waveform by copying the waveform to Excel, finding the average value over the rise time (0.0014ms). So, I got Ig(avg) = 10.9mA. I plugged this in the equation Ig = Qg/t_transition. We know from the IRFZ44N datasheet that at Vgs = 12V, Qg = 45nC. So, the equation yields t_transition = 4.1284us, which is not equal to the rise time from simulation (0.0014ms).

So, did I get the equation wrong?

Thank You

 

[Alec_t]

Your Vgs is 5V, the datasheet spec's is 12V. You're comparing apples with oranges .

 

[BlackMelon]

Your Vgs is 5V, the datasheet spec's is 12V. You're comparing apples with oranges .

Please look at the schematic again. I applied a 12V square wave to the gate via a resistor (purple trace).

 

[BlackMelon]

Sorry, my fault, the input is 12-0V pulse, not 5-0V. The schematic and simulation are correct. Just my typo.

 

[Alec_t]

I got Ig(avg) = 10.9mA.

LTspice sim gives a rise time of ~1.7uS and Ig(avg) ~ 28mA over that period!

 

[BlackMelon]

Is that the Vgs rise time, or the drain current's rise time? Nevertheless, none of us got the same result corresponding with the app note, right?

PS: Interpretation of the voltage source information in my schematic, see if we apply the same thing:
Let's begin from time 0. The voltage will travel from V1 to V2 (can be downward or upward). After that, it will stay constant at V2 for "PW" seconds, then it will travel back to V1. Subsequently, it will stay constant at V1 until the total time from the beginning is 1 period (PER), and so forth. TR and TF are the rise and fall times of the voltage level changes.

 

[Alec_t]

Is that the Vgs rise time

Yes.

Interpretation of the voltage source information in my schematic, see if we apply the same thing:

We do.


The end of the rise time is somewhat arbitrary in the sim, hence the average gate current is too.