Calculate Current, Power, EMS..

[evol_w10lv]

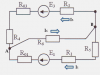
I have to calculate 1. current in each branch, 2. voltameter result 3. electromotive force (EMS) mode and 4. power bilance.
And need to use four methods:
Node Voltage Analysis (Node potential method)
Superposition Method
Loop Current Analysis
Kirchoff's Rules Analysis

I hope you can rede something or give me advices. What would be the right way to start?
Then I could try to calculate the tasks with your help..
Please.

 

[Laplace]

The wiring diagram specifications provide four different circuits. Draw the circuits individually with the specific values given for each case, leaving out the components that do not apply, and there is no need to draw the voltmeter for the circuit analysis. For the case requiring nodal analysis, identify and label the nodes. For loop analysis, identify and label the loops. I would label the '+' and '-' terminals of the voltage sources but you may be more comfortable with the arrows. (I would assume that the R01 is the internal resistance of the E1 voltage source. If that is the case then the R01-E1 node would be internal and not accessible.) Just remember there are four different circuits and four different problems here.

 

[evol_w10lv]

Yes, R01, R02, R03 are internal resistances.
But why there are four loops? Maybe I don't understand something, but I guess, that, when switch is OFF, then we don't have to use R02, R2 and E2, and of course we don't have to use voltmeter.
And then there could be two loops like this:

Or am I wrong?
And when switch is ON, then there could be three loops, because, as you mentioned, we don't have to use voltmeter.
I'm confused. When I will know, how exactly there are loops, then I could try to start calculations.

 

[Laplace]

OK, the redrawn circuit looks good to me, but that may just be the tequila talking. Note there are three possible current loops. Upper, Lower, and Outer loops. When choosing loops the only requirement is that every component must have at least one loop current passing through it. You have chosen the upper and lower loops to meet the requirement. Now write the loop equations.

 

[evol_w10lv]

Heh, I don't know what, but I did something wrog.
I tried Nr.32 using Kirchoff's rules analysis/method.

I got system of:
I5+I1-I4-I3-I6=0
I6-I5-I1=0
-E3=I3R3 - I6R6 + I4R4
E1 = I6R6 + I5R5 + I1R1

A, B - nodes. What I did wrong?
And also do I have to count R1+R01, R2+R02 and R3+R03 to get R on whole branch, because they are on chain?
Also, to get result of voltmetre, I have to count E1+U1+U01?
Tomorrow I will try other methods, but I want to know, what I did wrong using Kirchoff's rules.

 

[Laplace]

In your diagram there are branch currents I3 & I4 and I1 & I5. But I3 is the same current as I4 and I1 is the same as I5. Does it really make sense to write equations using I4 and I5, and then have to write additional equations I4=I3 and I5=I1? It would also simplify the algebra, at least for the purposes of calculating the branch currents, if you combined all series resistors into a single one and write the equations with a single resistor instead of three (I did not do that in the attached example because I have a computer algebra system that does all the grunt work.)

Apply KVL around each closed path, then apply KCL at nodes A & B. That will give three equations to solve for three currents: I1, I3, & I6. Note that I changed the direction of I3 to align with the polarity of the voltage source. Maybe you can keep the proper signs straight when following the closed path but I can't do it with any reliability for negative flows.

 

[evol_w10lv]

I count R03+R3 = 0.1 + 3.9 = 4, same as R01+R1 = 4 (let it be R3 and R1, but just without R01 and R03)
Then:
I6R6+I3R3+I4R4 = E3
-I1R1-I5R5-I6R6=-E1
I6-I1-I3=0
As I5=I1 and I3=I4 (as you metioned), then is system of:
10I1+3I6=40
9I3+3I6=28
I6-I1-I3=0

When I solve it, I get I1=I5= 2.7A; I3=I4= 1.7 A; I6= 4.4 A
Is it wright as your calculations with your algebra system?

Then I tried to solve this task with Node Voltage Analysis (Node potential method).
R(upper) = R3+R03+R4=9, R(lower) = R1+R01+R5 = 10 and R6 = 3
U(ab)= (E1*(1/Rlower) + E3*(1/Rupper))/((1/Rlower)+(1/Rupper)+(1/R6)) = (40*(1/10) + 28*(1/9))/((1/10)+(1/9)+(1/3)) = 13.1 V
I6 = (U(ab))/R6 = 13.1/3 = 4.6 A
But, when I tried to solve other I1, I3, I4, I5 ... results were differet as they had been solved by Kirchoff's Rules before. Only I6, as you can see, match. What's wrong again?

Also, can you chek other task? This ir much easier, I just want to be sure.

E = E1 + E2 = 19 + 10.1 = 21.9V
R56 = 177
R23 = R2 + R3 = 814 + 254 = 1068
R2356 = 151.1
R(total) = R2356 + R1 + R4 = 151.8 + 121 + 521 = 793.8
I = E/R(total) = 29.1/793.8 = 0.037A
I = I1 = I4 = I2356
I2356= I23 + I5 + I6
U1 = I1 * R1 = 0.037 * 121 = 4.5 V
U4 = I4 * R4 = 0.037 * 521 = 19.3 V
U2356 = I2356 * R2356 = 0.037 * 151.8 = 5.6 V
I2 = I3;
U23 = U2356
U2+U3 = U5 = U6
I5 = U4/R5 = 5.6/326 = 0.017A
I6 = U6/R6 = 5.6/387 = 0.014A
I23 = I2356 - I5-I6 = 0.037-0.017-0.014 = 0.006A
U2 = I2 * R2 = 0.006*814 = 4.9V
U3= I3 * R3 = 0.006 * 254 = 1.5 V

Thanks for helping!

 

[The Electrician]

When I solve it, I get I1=I5= 2.7A; I3=I4= 1.7 A; I6= 4.4 A
Is it wright as your calculations with your algebra system?

Then I tried to solve this task with Node Voltage Analysis (Node potential method).
R(upper) = R3+R03+R4=9, R(lower) = R1+R01+R5 = 10 and R6 = 3
U(ab)= (E1*(1/Rlower) + E3*(1/Rupper))/((1/Rlower)+(1/Rupper)+(1/R6)) = (40*(1/10) + 28*(1/9))/((1/10)+(1/9)+(1/3)) = 13.1 V
I6 = (U(ab))/R6 = 13.1/3 = 4.6 A
But, when I tried to solve other I1, I3, I4, I5 ... results were differet as they had been solved by Kirchoff's Rules before. Only I6, as you can see, match. What's wrong again?

The only thing wrong with your calculations is that you haven't carried enough digits.

I get:

I1=I5= 2.6939A; I3=I4= 1.6599 A; I6= 4.3537 A

These results match up perfectly with the solution by the nodal method if you carry more digits in your calculations.

 

[evol_w10lv]

Please, can you tell your solution with nodal method or at least give me a few hints? Actually, I have calculated this task with Kirchoff's Rules method (as you saw my answers), but there is needed Nodal method as well to be sure with my solution, but I don't know how exactly I can get it with nodal method.

 

[Laplace]

In the nodal method you write the node equations for a circuit which are an application of KCL stating that the sum of all current leaving a node must be zero. For any node the node equation expresses the current for any path as the potential difference to an adjacent node multiplied by the conductance of the path. For set #32 there is node A and node B where some of the paths have voltage sources which shift the potential difference between node A and node B for that path. Note also that I have chosen to consider current leaving a node as positive current, and have chosen node B as the ground reference point (Vb=0). Therefore only one node equation (for node A) is necessary, summing all the currents leaving node A (for node B). Every term of the node equation has the form (Va-Vb)/(resistance of the path) where node A sometimes sees a higher potential difference to node B because of the direction of the voltage source, (Va-(Vb+En)/(resistance of the path). Solve the node equation for the node voltage Va then calculate the currents for each path. The currents will be identical to those calculated using direct application of Kirchoff's Laws, within the accuracy of rounding error. See attached example for node A. You should try writing the node equation for node B instead and see if you get the same answer for the path currents.

 

[The Electrician]

Also, can you chek other task? This ir much easier, I just want to be sure.

E = E1 + E2 = 19 + 10.1 = 21.9V
R56 = 177
R23 = R2 + R3 = 814 + 254 = 1068
R2356 = 151.1
R(total) = R2356 + R1 + R4 = 151.8 + 121 + 521 = 793.8
I = E/R(total) = 29.1/793.8 = 0.037A
I = I1 = I4 = I2356
I2356= I23 + I5 + I6
U1 = I1 * R1 = 0.037 * 121 = 4.5 V
U4 = I4 * R4 = 0.037 * 521 = 19.3 V
U2356 = I2356 * R2356 = 0.037 * 151.8 = 5.6 V
I2 = I3;
U23 = U2356
U2+U3 = U5 = U6
I5 = U4/R5 = 5.6/326 = 0.017A
I6 = U6/R6 = 5.6/387 = 0.014A
I23 = I2356 - I5-I6 = 0.037-0.017-0.014 = 0.006A
U2 = I2 * R2 = 0.006*814 = 4.9V
U3= I3 * R3 = 0.006 * 254 = 1.5 V

Thanks for helping!

The voltage shown in red above should be 29.1V, not 21.9V. Even though you have made this error, it appears that you in fact used 29.1V in your calculations. Your calculations seem to be essentially correct, except that, once again, you are not carrying enough digits in your calculations.

 

[evol_w10lv]

Thanks!
But I also have to calculate currents with Loop Current Analysis for that loop, when switch is ON:

Here I have example, but still I'm not sure, how to write these equations correctly:

I guess it can take just a minute for you.
I tried something like in example:
E3+E2=(R02+R2+R3+R03)*Ia - (R02+R2)*Ib
E1=(R6+R5+R1+R02)*Ic + R6*Ib
-E2=(R6+R4+R02+R2)*Ib - (R02+R2)*Ia + R6*Ic

Can you help to write equations correctly?

 

[The Electrician]

I guess it can take just a minute for you.
I tried something like in example:
E3+E2=(R02+R2+R3+R03)*Ia - (R02+R2)*Ib
E1=(R6+R5+R1+R01)*Ic + R6*Ib
-E2=(R6+R4+R02+R2)*Ib - (R02+R2)*Ia + R6*Ic

Can you help to write equations correctly?

The only error I see is in red above.

 

[evol_w10lv]

30+50=(0.2+3.8+2.9+0.2)*Ia - (0.2+3.8)*Ib
40=(4+5+3.9+0.1)*Ic + (0.2+3.8)*Ib
-50=(4+4+3.8+0.2)*Ib-(0.2+3.8)*Ia + 4*Ic
I solve that system and get:
Ia = 10.127A
Ib = -2.024 A (I guess, there is opposite current direction)
Ic = 3.7 A
Then:
I3=I03=Ia = 10.127A
I5=I1=I01=Ic = 3.7A
I6 = -Ib-Ic = -(-0.024)-3.7 = -1.676A
I4 = -Ib = -(-2.024) = 2.024A
I02 = I2= -Ib+Ia = -(-2.024)+10.127 = 12.151A

Is it wright?
Can you chek it and show solution using Kirchhoff's current law (KCL) method?
Please.

And also - to determine, what is result of voltmeter, I have to calculate U01+U1+E1?

 

[The Electrician]

30+50=(0.2+3.8+2.9+0.2)*Ia - (0.2+3.8)*Ib
40=(4+5+3.9+0.1)*Ic + (0.2+3.8)*Ib
-50=(4+4+3.8+0.2)*Ib-(0.2+3.8)*Ia + 4*Ic
I solve that system and get:
Ia = 10.127A
Ib = -2.024 A (I guess, there is opposite current direction)
Ic = 3.7 A
Then:
I3=I03=Ia = 10.127A
I5=I1=I01=Ic = 3.7A
I6 = -Ib-Ic = -(-0.024)-3.7 = -1.676A
I4 = -Ib = -(-2.024) = 2.024A
I02 = I2= -Ib+Ia = -(-2.024)+10.127 = 12.151A

Is it wright?

For the equations as you have set them up here, I get the same solution.

Can you chek it and show solution using Kirchhoff's current law (KCL) method?
Please.

If you want help on a nodal solution. you should add to your diagram some additional details. Let the right end of your voltmeter (bottom right corner of the schematic) be your ground (reference node); show a ground symbol there. Then show (and number) 3 nodes--top of R4, bottom of R4 and top of R5. Get rid of the red current loops. Post that picture and then we'll discuss a nodal solution.

A nodal solution is going to be much less appropriate because all your sources are voltage sources instead of current sources.

And also - to determine, what is result of voltmeter, I have to calculate U01+U1+E1?

Yes.

 

[evol_w10lv]

Actually, there is no need for other method if Loop Current Analysis equations were right. [as you mentioned]. I just wanted to be sure, but I will believe and hope, that there is all OK.
But when we reconnect voltmeter, we get that diagram or not?

I guess that bottom corners are nodes, because there is votmeter or I'm wrong?

I just started to think, that if now I'm wrong, that all these solutions when switch is OFF are wrong in this case:

because there is no bottom nodes.
What's the truth? I have got lack of understanding.

 

[The Electrician]

There doesn't have to be a black dot on the diagram in order to have a node. There is a node between R1 and R5, between E1 and R1, between R01 and E2, et cetera.

Your solution in post #7 with the switch open was correct, as far as I could tell.

 

[evol_w10lv]

Despite that I believe, that solution in post #14 is wright. I tried to solve it with KCL method.

I1*(R5+R01+R1) + I6*R6 = E1
-I6*R6 + I4*R4 + I2*(R02+R2) = E2
-I2*(R2+R02) + I3*(R03+R3) = -E2-E3
A] -I2 + I4 - I3=0
B] -I4 - I6 + I1 =0
C] -I1 + I6 + I2=0

I didn't include I01, I02, I03, I5, because
I1 = I01 = I5
I02 = I2
I3 = I03

But I guess something is missing to solve that system. Can you look at it, what's there is wrong? For me it's easier to try to use this KLC method, that's why I don't want use nodal solution, but of course we can try if it's necessary and you shouldn't suggest, what's wrong in KLC equations.

For the same time I want to ask question for other task.
I have got this solution with nodal method.

When I calculate, I get:
fi1 = -10.14 V
fi2 = 3.39 V
fi3 = 20.37 V
Actually, you don't have to recalculate. It's no matter about numbers. Can you tell, how exactlly I can get I1, I2, I3, I4, I5 and I6, using R, E and fi?

 

[The Electrician]

I can't look at the first part for a few hours.

For the same time I want to ask question for other task.
I have got this solution with nodal method.

When I calculate, I get: I get the values in red. I'll check further in a few hours.
fi1 = -10.14 V -8.2877
fi2 = 3.39 V .0185
fi3 = 20.37 V 21.6043
Actually, you don't have to recalculate. It's no matter about numbers. Can you tell, how exactlly I can get I1, I2, I3, I4, I5 and I6, using R, E and fi?

I1 = (fi1-fi3+E1)/R1 (assuming I got the signs right)

You do the same thing for all the other currents. Take the voltage across the resistor and divide by the resistance of the resistor.

 

[Laplace]

Constructing the node equations with a slightly different method yields the same numerical result, see attached MathCAD page.