Butterworth function help request (mathematics)

[george2525]

Hello,

I have been having issues with the butterworth squared magnitude function for a while. I understand it enough to use it but its derivation is causing me a headache and realy bothers me. If anyone understands it mathematically it would be good to get some pointers.



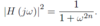
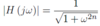
here are the typical Butterworth formulas in mosts texts.

Then comes the step where we should find the poles in the S domain. The following relation is often used:

I understand this

But what causes me confusion is that this is only true if s = jw. IE we have discarded the real parts of any poles (which we need)

Then the following is used to formulate the pole locations (on a circle)

Here is where I get lost. If we set w = S/j then doesnt |H(jw)|^2 become |H(S)|^2 ?

And if not, then why not? it is never written that way.

Also if we have already discarded the real parts of any poles by initially setting S = jw, then how do they magically re-appear in H(s)H(-S) to trace the classic butterworth pole circle?



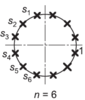
Maybe I have missed a mathematical rule somewhere?

I hope this question makes sense. If you are willing to help and need further clarification, please ask. Thanks to anyone who can help.

 

[Harald Kapp]

this is only true if s = jw.

This is a typical simplification made (and valid) for steady state signals.

If we set w = S/j then doesnt |H(jw)|^2 become |H(S)|^2 ?

It does. And by the same reasoning as in this equation:

where |H(jω)|² = H(jω)*H(-jω) it can also be written as |H(s)|² = H(s)*H(-s) = |H(jω)|²
I see no contradiction here.

And if not, then why not? it is never written that way.

Is it not? I don't know and I do not have an answer to that question.

how do they magically re-appear in H(s)H(-S) to trace the classic butterworth pole circle?

That is maybe due to sloppiness of the writer(s). It's simply easier to write 's' instead of 'jω' (I know because I had to use the windows symbol table to copy a small omega letter for this text).[/sup]

 

[george2525]

It does. And by the same reasoning as in this equation:

where |H(jω)|2 = H(jω)*H(-jω) it can also be written as |H(s)|2 = H(s)*H(-s) = |H(jω)|2
I see no contradiction here.

Thanks for the reply.

OK lets say H(S) = S
where S = A+jB

H(S)*H(-S) = (A+jB)(-A-jB) = B^2 - A^2 - j2AB

but |H(S)|^2 = A^2+B^2

which is not the same!

My point being that they are only the same IF A = 0

and so somewhere in the theory the real part of our poles (the A's) are brought back into the equation so we can properly place our poles. This is what I dont understand.

 

[Harald Kapp]

OK lets say H(S) = S
where S = A+jB

H(S)*H(-S) = (A+jB)(-A-jB) = B^2 - A^2 - j2AB

but |H(S)|^2 = A^2+B^2

which is not the same!

It is the same for s=jω as in that case A=0 and your equation reduces to
H(S)*H(-S) = (A+jB)(-A-jB) = B^2 - A^2 - j2AB = B²
compared to
|H(S)|^2 = A^2+B^2 = B²
which is identical. Keep in mind that the condition under which this holds true is s=jω which is valid for steady state signals only. In a strict sense there are no steady state signals as any practical signal has a time where it starts and a time where it ends. On the other hand this is a simplification that holds true when the duration of a signal is longer than the settling time of the system under consideration. A sufficiently long non-steady signal can then not be discerned from a steady signal. From the point of view of the system the signal is steady.

The mathematics as used in engineering obviously does not always follow the strict mathematical regimen - engineers are lazy, I should know