I would like to present a personal invention of mine.
It is a circuit that can produce a pseudo-random sequence with a period of 2^n numbers, where n is the numbers of registers.
The classical approach to generate pseudo-random numbers is to use Fibonacci or Galois linear-feedback shift register (LFSR) but the period of the generated random sequence is limited to 2^n - 1 numbers.
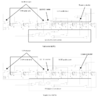
Furthermore, with the methodology I am proposing there are more circuit types that produce a complete sequence, therefore, it is more resistant to mathematical attacks.
Here it is a link to the blog post:
https://fdblog.xyz/circuits/nlprg-discussion/
Here to links to the code if someone wants to try it out:
https://gitlab.com/francescodellanna/nlprg
https://opencores.org/websvn/listing/nlprg/nlprg
I will post in the future the circuit with multiple bit lengths ( from 3 to 16 bits ).
Any feedback is really appreciated.
It is a circuit that can produce a pseudo-random sequence with a period of 2^n numbers, where n is the numbers of registers.
The classical approach to generate pseudo-random numbers is to use Fibonacci or Galois linear-feedback shift register (LFSR) but the period of the generated random sequence is limited to 2^n - 1 numbers.
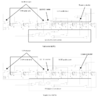
Furthermore, with the methodology I am proposing there are more circuit types that produce a complete sequence, therefore, it is more resistant to mathematical attacks.
Here it is a link to the blog post:
https://fdblog.xyz/circuits/nlprg-discussion/
Here to links to the code if someone wants to try it out:
https://gitlab.com/francescodellanna/nlprg
https://opencores.org/websvn/listing/nlprg/nlprg
I will post in the future the circuit with multiple bit lengths ( from 3 to 16 bits ).
Any feedback is really appreciated.
