why do we use average power for capacitor?

[komalbarun]

Energy stored = 1/2 x C x V x V = 0.5 x C x V^2
E = 0.5 x C x V^2

V = Energy (measured in joules W) / Electric charge (Q) = W / Q
V = W / Q

That means that if I have a 9V battery, it will apply an E of 9W to each Q.

If I have a capacitor with a capacitance C of 2F and charge it to V = 9, then Q stored is = 2F X 9V = 18 Q (Since Q stored is C x V).

This implies that, since P = I x V, where I = Q / seconds and assuming seconds = 1 then I = Q.

so P = Q per 1 sec x V = 18 x 9 = 162 Watts should be stored ( since when connected the capacitor should apply 9W of energy to each Q(charged to 9V))
also C x V^2 = 2 x 9 x 9 = 162,

therefore P = Q per 1 sec x V = C x V^2, thus we can rewrite energy stored in capacitor as:

E = 0.5 X P


Where does the 0.5 come from??
sorry for any mistakes in above theories and counting on your help, thanks

 

[BobK]

It comes from integration.

Bob

 

[komalbarun]

is there a better explanation than "it comes from integration" I am pretty weak at integration, unless its shown line by line xD.

 

[komalbarun]

is there a better explanation than "it comes from integration" I am pretty weak at integration, unless its shown line by line xD.

and euh...what do we integrate x_x?

 

[woodchips]

I think this is one of those conundrums sent to worry engineers. As far as I can remember when charging a capacitor half the energy ends up in the capacitor, and half is lost in the wiring resistance. There is a nice explanation somewhere, just can't remember where.

 

[duke37]

I do not follow your first post.
Energy is measured in joules.
Watts are a measurement of power.

The power you can get from a capacitor depends on how quickly you can charge it and discharge it. Switch mode power supplies use high frequencies to get high power throughput. You cannot extract all the energy from a capacitor, perhaps only 10% would be extracted or the voltage would drop too low.

 

[komalbarun]

I do not follow your first post.
Energy is measured in joules.
Watts are a measurement of power.

The power you can get from a capacitor depends on how quickly you can charge it and discharge it. Switch mode power supplies use high frequencies to get high power throughput. You cannot extract all the energy from a capacitor, perhaps only 10% would be extracted or the voltage would drop too low.

why is the energy stored 0.5 x C x V x V and not C x V x V?
Normally P = C x V x V, so where the 0.5 comes from and why use it?

I think its because the capacitor voltage decreases wrt time and as the voltage decreases, lesser and lesser power is available but am not sure about this even though I tested this theory and it is pretty consistent (view attachment [capacitor fully charged V = 1V in attachment]).

 

[BobK]

Why is the area of a right triangle only 1/2 base * height?

This is not an impertenent question. It is for eactly the same reason. When we charge a capacitor with a constant current, the voltage / time looks like a triangle. The energy put into the capacitor is the integral of the V * I over the charging time. Since this is a triangle, the area under the curve (which is what integration is) is the area of the triangle and hence the 1/2.

In case you know a little physics, the energy of a mass m accelerated to an velocity v is 1/2 m*v*v again for the same reason.

Bob

 

[john monks]

komalbarun, if you have a capacitor and you impress a given current across it you have a constantly changing voltage across the capacitor. And the power going into the capacitor at any given moment is voltage X current. And energy is watts per second. So for example if I have a 1 farad capacitor starting out at 0 volts and I impress 1 ampere of current through it I will develop 1 volt across it in 1 second. So what do I do? To find the total energy in the capacitor after 1 second i integrate my voltage and current for 1 second. So what do I get? I integrate my voltage amperage or power for one second and I get 1/2 joules.
Look at it this way:
I=CVdV
P=IV
E=PT
So if we integrate CVdV we get 0.5 x C x C plus your original value which was zero.

To check if I am on the right track I can differentiate 1/2CV^2 and I get CV.

If my explanation is weak I can take a different approach.

 

[Laplace]

One method of finding the exact value of the energy stored in a capacitor involves integration of an exponential function. See attachment.

 

[komalbarun]

One method of finding the exact value of the energy stored in a capacitor involves integration of an exponential function. See attachment.

how do you get (Vo x e^-t/t)^2/R?
When i do it i get (Vo^2 x e^-t/t)/R.

 

[komalbarun]

komalbarun, if you have a capacitor and you impress a given current across it you have a constantly changing voltage across the capacitor. And the power going into the capacitor at any given moment is voltage X current. And energy is watts per second. So for example if I have a 1 farad capacitor starting out at 0 volts and I impress 1 ampere of current through it I will develop 1 volt across it in 1 second. So what do I do? To find the total energy in the capacitor after 1 second i integrate my voltage and current for 1 second. So what do I get? I integrate my voltage amperage or power for one second and I get 1/2 joules.
Look at it this way:
I=CVdV
P=IV
E=PT
So if we integrate CVdV we get 0.5 x C x C plus your original value which was zero.

To check if I am on the right track I can differentiate 1/2CV^2 and I get CV.

If my explanation is weak I can take a different approach.

please try with a different approach.

 

[john monks]

It has been shown experimentally that the charge on a capacitor is equal to the capacitance times the voltage. And if you charge a 1 farad capacitor to 1 volt for one second you need a current of 1 ampere. So the voltage increases as the current is applied to the capacitor. The power needed to charge the capacitor is voltage times amperage. And the energy is power times time in seconds. So here we go:
P=IV
E=PT
Q=CV. C is capacitance.
So what we want to do is integrate the charge, Q.
So energy, E equals the integral of QdV which is the integral of CVdV or 1/2 x CV^2.

Let me think about this so I can explain it in a simpler fashion.
One thing I learned from my physics professor was not to get hung up with the math. And it seems to me that everyone that has problems understanding these concepts has a problem with the physics not the math. If you have a problem with the calculus I will try to explain this by using the average charge on a capacitor during the charging process.

 

[komalbarun]

It has been shown experimentally that the charge on a capacitor is equal to the capacitance times the voltage. And if you charge a 1 farad capacitor to 1 volt for one second you need a current of 1 ampere. So the voltage increases as the current is applied to the capacitor. The power needed to charge the capacitor is voltage times amperage. And the energy is power times time in seconds. So here we go:
P=IV
E=PT
Q=CV. C is capacitance.
So what we want to do is integrate the charge, Q.
So energy, E equals the integral of QdV which is the integral of CVdV or 1/2 x CV^2.

Let me think about this so I can explain it in a simpler fashion.
One thing I learned from my physics professor was not to get hung up with the math. And it seems to me that everyone that has problems understanding these concepts has a problem with the physics not the math. If you have a problem with the calculus I will try to explain this by using the average charge on a capacitor during the charging process.

true indeed, awaiting your simpler fashion and trying to understand this post. Thanks in advance.

 

[john monks]

These concepts are difficult to explain but let's try this. In an example where you are charging a capacitor with a constant current for a fixed time period you get a voltage at the end of this time and therefore you are pumping in a certain power at this end time of voltage times current. Now if you change your current you change the voltage proportionately. So as the voltage is higher the current is higher and this is where you get the voltage squared from V^2. you can think of the current as being some K factor of the voltage K*V.
When you are looking at the power going into the capacitor you are looking at the average power going into the capacitor for your time frame IV. So you are starting at some current times zero volts at one end plus some voltage time some current divided by two. This is where you get the 1/2 from. So let's look at some math.

P=power
V=voltage
Vi=initial voltage at time zero
I=current
So P=(ViI+VI)/2=VI/2

Lest say that your constant current is some K factor of your final voltage I=KV and the energy is proportion a to the capacitance C.

So P=(ViKV+VKV)C/2=(1/2)CV^2

The difficulty I have is not in understanding the physics it is converting the English into mathematics. This is called "setting up the problem". And this is the most difficult part. And from hanging around the colleges it is crystal that nearly all physics and electronics students do not have a big problem with the mathematics that they think they do. It is the comprehension of the physics. So keep in mind the physics comes first not the math. That is mathematics is subject to the physics. Not the other way around.

 

[(*steve*)]

(and I've painted myself into a corner somewhere...

If someone can find the error in my "simple" explanation, I'd appreciate it)

Let me have a try.

Energy stored = 1/2 x C x V x V = 0.5 x C x V^2
E = 0.5 x C x V^2

Where does the 0.5 come from??

I realise the above is somewhat truncated, but I trust that satisfying the shortened version will satisfy the rest

OK, as I understand it, we're trying to find out why that 1/2 in the 1/2cv^2 comes from.

I wonder if I can do that graphically...

Not calculus (Playing fast and loose)

Whilst I'm not going to be using calculus, I cannot fail to mention a little (since a capacitor is defined in terms of a differential equation). So whilst I'll give you correct results, I'll be doing things that are mathematically wrong. They just happen to work with the equations I use them with... Specifically, when you see me start to convert things like dt into real numerical values, I'm doing a really bad thing.

dt refers to the smallest change in d, the limit as the change approaches zero. It is effectively a value so small that you can't distinguish it from zero, yet you can multiply and divide by it without it doing what zero does in these cases.

larger changes in d would be called delta-d, but I don't have a convenient delta sign on my keyboard Also, once you change dv to delta-v, you are committing the same grave mistake...

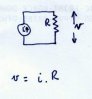
Resistor

Let's first look at a resistor:

OK, here is a simple circuit. We have a current source (some constant current i) flowing through a resistor r.

We know that the voltage across the resistor is the current multiplied by the resistance.

We know that, because that is a simple rearrangement of the definition of resistance (R = V/I).

Let's graph the voltage with respect to time.



Here we can see that the voltage across the resistor is constant (as we would expect)

The value is the same at t=0, 1, 2, 3, ...

Now, we know that we can calculate power as i * v. Remembering that power is an instantaneous value. We also know that i is constant (a given from above) and that v is constant (seen from the graph above).

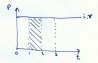
So we can draw a graph of power with respect to time:

What are we going to expect? if v = i * r, and p = v * r then p = i * i * r. Because we know that i and r are constant, the power remains constant.

And there we are i * v is constant and we get another horizontal line.

We also know that power is joules per second. And joules are energy.

So the shaded area represents the energy dissipated in 1 second. It is a rectangle with one side represented by time (1 second) and the other being the voltage.

So, we can confirm that if the power is a constant p watts, the energy is p joules per second. And that shaded rectangle has an area p.

This is very easy to calculate, so let's draw a table of energy with time. assuming it starts at 0 when t = 0

time | energy
-----+--------
  0  |    0
  1  |    p
  2  |   2p
  3  |   3p
  4  |   4p

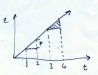
This looks very simple. The total energy is given by t * p, and we know p is constant, so let's graph it:

This time, the graph is not a straight horizontal line, but it is still a straight line.

The graph is now a linear function of time. e = t * p = t * i * v = t * i * i * r = t.i^2.r

And this allows us to calculate the energy used from the beginning of time to now.

But that's not too useful. We might want to calculate the energy between 2 times, say between t = 3 and t = 4.

Something we can tell from this graph is that we have a number of rectangles and triangles. Each triangle has a base of length t = 1, and a height of p. Essentially this is the definition of our graph. The total energy rises by p each second.

Power = i^2r, and total energy is i^2rt

Capacitor

Now let's look at a capacitor.

OK, here is a simple circuit. We have a current source (some constant current i) flowing through a capacitor c.

We know that the change in voltage across the capacitor per unit of time is the current divided by the capacitance.

We know that, because that is a simple identity which defines the behaviour of a capacitor. (you might have to just accept this).

We can rearrange that to look like this: dv = (i/c) dt

What this says (kinda) is that the change in voltage is equal to the current times the capacitance times the difference in time.

We can graph this! But lets make a table of values first. dt is just a small change in time, so we can represent time as 0, dt, 2*dt, 3*dt,

time | dt |   dv
-----+----+--------
   0 |    |
  dt | dt | i.dt/c
 2dt | dt | i.dt/c
 3dt | dt | i.dt/c
 4dt | dt | i.dt/c

Let's graph the change in voltage with respect to change in time.

To do this, I'm just going to take the graph we used for voltage versus time for a resistor and make a few small changes.

Note that the graphs are the same, except what a resistor does with voltage and time, a capacitor does with changes in voltage and time. (This should spin your mind a little. Don't worry. The important thing is that the graphs look the same)

This is pretty simple. Note that our table doesn't have a value at t = 0, but just believe me that when you graph all the points you get a straight line.

OK, but we're not even at the first step yet.

What we want to show is the voltage with respect to time. For that we need to make an assumption.

Let's assume that the voltage on the capacitor is zero at time = 0. This might sound like a huge assumption, but zero time could be the beginning of time, or it could be now, or last Tuesday at 1 pm, or some time tomorrow. What is important is that at that time the capacitor voltage was zero, and that the other constraints are still valid (same capacitance and same current). Essentially we're picking the time when the voltage was zero.

With this constraint in mind, we can just make a few trivial adjustments to the last table.

time | dv  |   v
-----+-----+--------
  0  | i/c |  0
  1  | i/c | i/c
  2  | i/c | 2i/c
  3  | i/c | 3i/c
  4  | i/c | 4i/c

Now when we graph this we get:

Well, that was pretty simple.

You need to step back and notice three things:

1) It's a straight line
2) it's NOT the same as the graph for V vs t for a resistor.
3) it IS similar to another graph for a resistor...

What is it's equation?

From inspection of the table above, you should be able to see that it is v = i.t/c.

We also know that charge is a function of current and time. So we also know that Q = it, and thus if v = it/c and Q = it, then V = Q/c (which very nicely gets rid of the t term)

OK, so power is a bit unusual when we talk about capacitors, but let's press on with it.

That graph above shows v, now we want to show p.

p = i * v

I've broken it below here somewhere...

Again, we know that everything but t is constant (and v is linear in terms of t), so the graph looks like this:

Again, I've modified an earlier graph (and i dv is wrong).

Recall what we did for a resistor at this step:

So the shaded area represents the energy dissipated in 1 second. It is a rectangle with one side represented by time (1 second) and the other being the voltage.

So, we can confirm that if the power is a constant p watts, the energy is p joules per second. And that shaded rectangle has an area p.

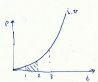
In this case, The power is not constant, but rising, and at each instant the energy is p joules per second.

Now, the accumulated power is not a rectangle, it is a triangle.

What we showed with the resistor example is that the area under the curve represented energy.

So is we want to graph energy with respect to time for a capacitor, we need to graph how the total area changes with time.

And what is the total area? It is the triangle with the base extending from the origin to some time t, and a height given by v.

We know that the area of a triangle is 1/2 base * height, so

e = 1/2.t.v = 1/2.t.i^2.t/c = 1/2.i^2.t^2/c

So we get a function of the form:

e = (i^2.t^2)/2c.

This looks complex, and since we know that everything but t is a constant, the function is of the form e = kt^2

and that should be energy, not power...

 

[Laplace]

Instead of finding capacitor energy using an exponential discharge model, one can use a constant current charge model. See attachment.

It is debatable that the mathematics is subject to the physics. The models one uses to explain the physics are definitely subject to the mathematics. If that is not true, then the model is wrong, i.e., not appropriate for the physics.

 

[(*steve*)]

Hey Laplace... I was working on the "simple" explanation using that approach (but without explicitly invoking integrals). Can you see where I borked it?

 

[komalbarun]

Instead of finding capacitor energy using an exponential discharge model, one can use a constant current charge model. See attachment.

It is debatable that the mathematics is subject to the physics. The models one uses to explain the physics are definitely subject to the mathematics. If that is not true, then the model is wrong, i.e., not appropriate for the physics.

Thnx to everyone.

 

[Laplace]

Hey Laplace... I was working on the "simple" explanation using that approach (but without explicitly invoking integrals). Can you see where I borked it?

The voltage vs time graph and the power vs time graph for the charging capacitor are both straight lines. Your last graph with the curved line claims to show power but the line shows energy (as you realized and should have corrected).