The calculus of FM super heterodyne receiver.
I found an interesting problem in my calculus text book. The instructor skipped this section in the text book because it is using the graphing calculator to help with the calculus and my instructor is opposed to doing that.
Well so I'm looking at an example the book gave. I would like a conceptual understanding of this book's example to help me understand how FM radio receiver works. The calculus text book Single Variable Calculus Early Transcendentals is by James Stewart. The edition is 7th edition. The chapter I am in is chapter 4. The chapter section I am in is 4.6
So the example problem starts with a function and uses the first derivative test and the second derivative test with the graphing calculator to get the graph of the function as well as the graphs of the composition of functions that create the FM modulated function.
The function is of the family of functions f(x) = sin ( x + sin(cx) ), where c = 2.
So the function we want to graph is f(x) = sin ( x + sin(2x) )
So when we first graph it on the graphing calculator we get an inaccurate graph that looks something like this:
So the first derivative is f ' (x) = cos ( x + sin2x) * ( 1 + 2cos2x), using the chain rule.
So then the book says that using zooming in on the graphing calculator with the first derivative test, we find the following approxiamate values for f(x):
Intervals of increase: (0, 0.6), (1.0, 1.6), (2.1, 2.5)
Intervals of decrease: (0.6, 1.0), (1.6, 2.1), (2.5, pi)
Local maximum values: f(0.6) =~ 1, f(1.6) =~1, f(2.5) =~1
Local minimum values: f(1.0) =~0.94, f(2.1) =~0.94
So the second derivative is f " (x) = - sin ( x + sin2x) * (1 + 2cos2x) + cos (x + sin2x) * (-2sin2x * 2), using the chain rule and the product rule
= f " (x) = -sin ( x + sin2x) * (1 + 2cos2x) + cos (x + sin2x) * (-4sin2x), simplifying
= f " (x) = -sin ( x + sin2x) * (1 + 2cos2x) - 4sin2x * cos (x + sin2x)
= f " (x) = -( (1 + 2cos2x)) * (sin ( x + sin2x) - 4sin2x * cos (x + sin2x)
So the book says that graphing the second derivative, we find the following approxiamate values for f(x) :
Concave upward on: (0.8, 1.3), (1.8, 2.3)
Concave downward on: (0, 0.8), (1.3, 1.8), (2.3, pi)
Inflection points: (0, 0), (0.8, 0.97), (1.3, 0.97), (1.8, 0.97), (2.3, 0.97)
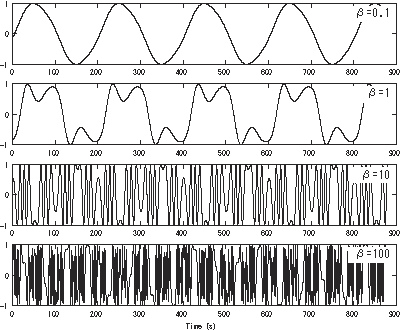
So now we can sketch the graph by hand of f(x) for a more accurate graph and it looks something like this (Wikipedia used different values of C, such as 0.1, 10, and even 100):
Zoomed in it looks something like this:
I think the wave will look different and will look something like this if a different c value is used:

So what c value is used in the FM broadcast band from 88MHZ to 107.9MHZ? Google failed to answer my question. Wikipedia says that narrow band FM radio uses a lower order modulation index of c < 1 resulting in a frequency change of 2.5 khz above and 2.5 khz below the center frequency for a bandwidth to carry human speech of 3.5 khz bandwidth. Wikipedia says that wide band FM radio uses a higher order modulation index of c>1 resulting in a frequency change of 75 khz above and 75 khz below the center frequency for a bandwidth to carry music of up to 20khz bandwidth. So is the challenge of finding a good modulation index to use for FM, is the challenge to replicate the full frequency response of the human ear (20khz bandwidth) at a minimum bandwidth to optimize bandwidth so that neighbooring stations do not interfer and more stations can transmit in the same city? Is this why FM uses VHF instead of MW for bandwidth optimization so that nearby stations do not interfer since the shorter wavelength waves don't travel as far so a higher order modulation index can be used with out worrying about interference? From the Wikipedia article, it appears that to calculate the effective bandwidth of a modulation index for FM you have to solve a differential equation with integrals in it, and I am only in calc I so I can't solve these equations, so I let Wikipedia solve it for me.
Wouldn't an FM receiver only receive stations that use the same modulation index c that the receiver understands?
Which would have less distortion from EMI, lower value of modulation index c or higher value of modulation index c?
So FM radio reciever is taking derivatives of frequency harmonics generated by the feedback of tubes or transistors (sort of) and that is why the mixer it uses is called a "differentiator"?
So is this why FM radio only works with a super heterodyne technique employed in the detector and does not work with a regenerative technique or crystal technique employed in the detector?
So in the AM super heterodyne receiver, the super heterodyne technique employed in the detector is to greatly increase the gain without an audible feedback squel, improve the frequency selectibility, and reduce the interference of nearby stations, correct? Compared to in the AM regenerative receiver, the regenerative technique employed in the detector greatly increases the gain but the gain is limited to below over drive when in AM mode instead of CW mode or else an audible feedback squel is heard (which is turned on and off to generate CW Morse code beeping), correct?
I have heard of a "super regenerative receiver" on the internet that can receive FM. So does this mean that the super heterodyne technique is used to convert the FM into AM that the regenerative detector can receive?
So can an FM radio receiver use any detector, even crystal detector, to demodulate AM to audio, as long as the FM has already been converted to AM by the super heterodyne technique?
Wikipedia says that FM is used in VHS. So does that make the video quality of VHS superior to that of analog TV (since analog TV video signal uses AM)? Does that also make the audio quality of VHS comparable to the audio quality of CDs if a higher order modulation index capable of replicating the full frequency range of human hearing was used and superior to vinly because vinly uses unmodulated audio AM which AM is prone to noise?
Edit: I found in the Wikipedia article when I read it again that the ratio of original frequency to synthesized frequency in wideband stereo FM broadcast is 10,000 , compared to the ratio of original frequency to synthesized frequency in VHS is only 2. So I presume that VHS audio can not replicate the full frequency response of human hearing and VHS audio is mono, although it certainly has less hiss than vinly.
Edit 2: I found in the Wikipedia article about VHS that the audio is umodulated (base band) and is very prone to hiss, which is why Dolby encoding is used, but unfortunately all Dolby does is attempt to restore dynamic range to make the audio sound punchier resulting in the tape hiss also being increased in dynamic range, much the same as crystallizer algorithms used today to attempt to improve the quality of MP3 for MP3 encoded with a noise floor to decrease dynamic range in file storage to decrease file size, so really the quality is not improved, just most people can not tell the difference and ignore the amplified hiss and think it sounds punchier, resulting in most people can not tell the difference between Dolby encoding or MP3 encoding used with a crystalizer algorithm compared to uncompressed PCM audio.
So to receive the wideband stereo FM broadcast band, would a reciever have to be able to recieve at modulation index of 10,000 and would not recieve at a modulation index higher or lower?
Ratio of original frequency to synthesized frequency is the same as modulation index, right?
Okay just tell me if I'm in over my head in the calculus and nothing about FM will make sense since I'm not an engineering student who has taken Calc III and differential equations. Then I will just give up.
I found an interesting problem in my calculus text book. The instructor skipped this section in the text book because it is using the graphing calculator to help with the calculus and my instructor is opposed to doing that.
Well so I'm looking at an example the book gave. I would like a conceptual understanding of this book's example to help me understand how FM radio receiver works. The calculus text book Single Variable Calculus Early Transcendentals is by James Stewart. The edition is 7th edition. The chapter I am in is chapter 4. The chapter section I am in is 4.6
So the example problem starts with a function and uses the first derivative test and the second derivative test with the graphing calculator to get the graph of the function as well as the graphs of the composition of functions that create the FM modulated function.
The function is of the family of functions f(x) = sin ( x + sin(cx) ), where c = 2.
So the function we want to graph is f(x) = sin ( x + sin(2x) )
So when we first graph it on the graphing calculator we get an inaccurate graph that looks something like this:

So the first derivative is f ' (x) = cos ( x + sin2x) * ( 1 + 2cos2x), using the chain rule.
So then the book says that using zooming in on the graphing calculator with the first derivative test, we find the following approxiamate values for f(x):
Intervals of increase: (0, 0.6), (1.0, 1.6), (2.1, 2.5)
Intervals of decrease: (0.6, 1.0), (1.6, 2.1), (2.5, pi)
Local maximum values: f(0.6) =~ 1, f(1.6) =~1, f(2.5) =~1
Local minimum values: f(1.0) =~0.94, f(2.1) =~0.94
So the second derivative is f " (x) = - sin ( x + sin2x) * (1 + 2cos2x) + cos (x + sin2x) * (-2sin2x * 2), using the chain rule and the product rule
= f " (x) = -sin ( x + sin2x) * (1 + 2cos2x) + cos (x + sin2x) * (-4sin2x), simplifying
= f " (x) = -sin ( x + sin2x) * (1 + 2cos2x) - 4sin2x * cos (x + sin2x)
= f " (x) = -( (1 + 2cos2x)) * (sin ( x + sin2x) - 4sin2x * cos (x + sin2x)
So the book says that graphing the second derivative, we find the following approxiamate values for f(x) :
Concave upward on: (0.8, 1.3), (1.8, 2.3)
Concave downward on: (0, 0.8), (1.3, 1.8), (2.3, pi)
Inflection points: (0, 0), (0.8, 0.97), (1.3, 0.97), (1.8, 0.97), (2.3, 0.97)
So now we can sketch the graph by hand of f(x) for a more accurate graph and it looks something like this (Wikipedia used different values of C, such as 0.1, 10, and even 100):

Zoomed in it looks something like this:

I think the wave will look different and will look something like this if a different c value is used:

So what c value is used in the FM broadcast band from 88MHZ to 107.9MHZ? Google failed to answer my question. Wikipedia says that narrow band FM radio uses a lower order modulation index of c < 1 resulting in a frequency change of 2.5 khz above and 2.5 khz below the center frequency for a bandwidth to carry human speech of 3.5 khz bandwidth. Wikipedia says that wide band FM radio uses a higher order modulation index of c>1 resulting in a frequency change of 75 khz above and 75 khz below the center frequency for a bandwidth to carry music of up to 20khz bandwidth. So is the challenge of finding a good modulation index to use for FM, is the challenge to replicate the full frequency response of the human ear (20khz bandwidth) at a minimum bandwidth to optimize bandwidth so that neighbooring stations do not interfer and more stations can transmit in the same city? Is this why FM uses VHF instead of MW for bandwidth optimization so that nearby stations do not interfer since the shorter wavelength waves don't travel as far so a higher order modulation index can be used with out worrying about interference? From the Wikipedia article, it appears that to calculate the effective bandwidth of a modulation index for FM you have to solve a differential equation with integrals in it, and I am only in calc I so I can't solve these equations, so I let Wikipedia solve it for me.
Wouldn't an FM receiver only receive stations that use the same modulation index c that the receiver understands?
Which would have less distortion from EMI, lower value of modulation index c or higher value of modulation index c?
So FM radio reciever is taking derivatives of frequency harmonics generated by the feedback of tubes or transistors (sort of) and that is why the mixer it uses is called a "differentiator"?
So is this why FM radio only works with a super heterodyne technique employed in the detector and does not work with a regenerative technique or crystal technique employed in the detector?
So in the AM super heterodyne receiver, the super heterodyne technique employed in the detector is to greatly increase the gain without an audible feedback squel, improve the frequency selectibility, and reduce the interference of nearby stations, correct? Compared to in the AM regenerative receiver, the regenerative technique employed in the detector greatly increases the gain but the gain is limited to below over drive when in AM mode instead of CW mode or else an audible feedback squel is heard (which is turned on and off to generate CW Morse code beeping), correct?
I have heard of a "super regenerative receiver" on the internet that can receive FM. So does this mean that the super heterodyne technique is used to convert the FM into AM that the regenerative detector can receive?
So can an FM radio receiver use any detector, even crystal detector, to demodulate AM to audio, as long as the FM has already been converted to AM by the super heterodyne technique?
Wikipedia says that FM is used in VHS. So does that make the video quality of VHS superior to that of analog TV (since analog TV video signal uses AM)? Does that also make the audio quality of VHS comparable to the audio quality of CDs if a higher order modulation index capable of replicating the full frequency range of human hearing was used and superior to vinly because vinly uses unmodulated audio AM which AM is prone to noise?
Edit: I found in the Wikipedia article when I read it again that the ratio of original frequency to synthesized frequency in wideband stereo FM broadcast is 10,000 , compared to the ratio of original frequency to synthesized frequency in VHS is only 2. So I presume that VHS audio can not replicate the full frequency response of human hearing and VHS audio is mono, although it certainly has less hiss than vinly.
Edit 2: I found in the Wikipedia article about VHS that the audio is umodulated (base band) and is very prone to hiss, which is why Dolby encoding is used, but unfortunately all Dolby does is attempt to restore dynamic range to make the audio sound punchier resulting in the tape hiss also being increased in dynamic range, much the same as crystallizer algorithms used today to attempt to improve the quality of MP3 for MP3 encoded with a noise floor to decrease dynamic range in file storage to decrease file size, so really the quality is not improved, just most people can not tell the difference and ignore the amplified hiss and think it sounds punchier, resulting in most people can not tell the difference between Dolby encoding or MP3 encoding used with a crystalizer algorithm compared to uncompressed PCM audio.
So to receive the wideband stereo FM broadcast band, would a reciever have to be able to recieve at modulation index of 10,000 and would not recieve at a modulation index higher or lower?
Ratio of original frequency to synthesized frequency is the same as modulation index, right?
Okay just tell me if I'm in over my head in the calculus and nothing about FM will make sense since I'm not an engineering student who has taken Calc III and differential equations. Then I will just give up.
Last edited:
