Solenoid Current Flow

[Mark34]

Hello, I want to calculate the theoretical magnetic field strength in a Solenoid by discharging a Capacitor into it. So magnetic field strength B = u * N/L * I , but how do I calculate I (current) ?
Lets say I have 300V 1000microfarad Capacitor, so energy stored W is 45 Joules or Watts.
I = P/V so current = 45W/300V = 0.15 Amps, is this correct I have 0.15 Amps flowing in the Solenoid?

 

[Alec_t]

so current = 45W/300V = 0.15 Amps

No. Instantaneous current will vary as a function of coil inductance, coil resistance and the equivalent series resistance of the capacitor. If the solenoid has a moving ferromagnetic core then the coil inductance will vary with time.

 

[Mark34]

So how do I calculate I (current) if I have the coil inductance and coil resistance value ? Solenoid has no ferromagnetic core, it is empty and I want to calculate only the initial maximum I (current).

 

[Mark34]

I found this http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capdis.html initial I = V/R so I (current) = 300V / 3ohm = 100Amps

 

[Alec_t]

So how do I calculate I (current) if I have the coil inductance and coil resistance value ?

I'm sure someone here can do the maths, but I just let LTspice do it for me :-

Unless the cap's ESR is unusually high the initial current (here, 5A for a coil with resistance 50Ω) is dominated by the coil's resistance.
BTW, it's not wise to charge a 300V rated cap to anywhere near that voltage if you want the cap to have a long life.

 

[Mark34]

Thanks for the reply, the capacitor is 400V I use it at 300V and the Coil resistance is 3ohms.

 

[crutschow]

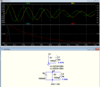
Below is my LTspice simulation:
The current (yellow trace) starts at zero since current can't instantly start in a inductor (you have to use the uic option in the transient simulation).
It then rises to the resonant peak (here about 7.3A simulated) where the capacitance voltage (green trace) is zero and all the capacitor energy has been transferred to the inductor current (minus any resistive losses).
Since this is a lossy resonant circuit it will continue to have a decaying oscillation, with the energy being transferred back and forth between the capacitor voltage and the inductor current (note the 90° phase difference between voltage and current), until all the energy is dissipated in the circuit parasitic resistances.

If you don't want the circuit to oscillate (and also prevent the capacitor voltage from going negative which can damage an electrolytic), you can put a high-voltage diode in parallel with the capacitor (cathode to positive).
That will allow the inductor current to reach the maximum current (red trace) and then decay to zero as determined by the resistive and diode losses from the current.

An easy way to determine the peak current (ignoring the resistances) is to calculate at what current the inductor energy equals the original capacitor energy (1/2 CV² = 1/2 LI²).
That gives a value of 7.9A for this circuit.

 

[crutschow]

That will allow the inductor current to reach the maximum current (red trace) and then decay to zero as determined by the resistive and diode losses from the current.

Edit: That will allow the inductor current to reach the maximum current (red trace) where the capacitor voltage reaches zero and, at which point, the diode starts to carry the current, The current then decays to zero as determined by the resistive and diode losses from the current.

 

[Mark34]

I learned myself LTspice , calculated the inductance of my coil and its about 1 micro Henry and end up with this I think is more realistic because I read capacitors discharge into a coil very fast like 2-10 miliseconds. I don't know about the initial 80Amps.

 

[crutschow]

I read capacitors discharge into a coil very fast like 2-10 miliseconds.

Did you also read that the time depends upon the value of the capacitance and inductance?
1µH is a very low inductance.

 

[Harald Kapp]

@Mark34 : Your result is due to the comparatively high resistance (3 Ω) of the coil. When I use the default resistance (1 mΩ) I get this result:



To solve mathematically for the value of I and V over time one will have to solve a second order differential equation starting from these basic equations:
V = L × dI/dt for the inductor,
I = C × dV/dt for the capacitor
V = R × I for the resistance.
See e.g. here (in case you are interested in the theoretical aspect). The result is a damped sine with the frequency determined by sqrt(L × C) and the damping determined by R.

Admitted: using the simulator is the easier method, but knowing the math helps to understand what is going on - at least for me

 

[Mark34]

Thanks guys for the help.