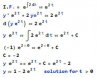Can someone help me to get started...
Problem:
dy/dt + 2y(t) = 2x(t) where x(t) = u(t) and y(0) = -1
I know the standard form of a diff eq is:
dy/dx+ P(x)y=Q(x)
and I know how to solve for y using the integrating factor if the equation is in the same model as the standard equation
The issue I am having in the given problem: it is not in the form of the standard equation.
I don't see that 2y(t) is = to P(x)y.
And beyond that, I am unclear on where to plug in the givens
Any help would be appreciated.
I've attached a PDF if that helps
Problem:
dy/dt + 2y(t) = 2x(t) where x(t) = u(t) and y(0) = -1
I know the standard form of a diff eq is:
dy/dx+ P(x)y=Q(x)
and I know how to solve for y using the integrating factor if the equation is in the same model as the standard equation
The issue I am having in the given problem: it is not in the form of the standard equation.
I don't see that 2y(t) is = to P(x)y.
And beyond that, I am unclear on where to plug in the givens
Any help would be appreciated.
I've attached a PDF if that helps