Maximum Power through a L-R circuit

[e21959]

Hi. someone may explain me how Maximum Power has been calculated in formula here in the image?
Watt = V*I or V^2/R.or Vmax*Imax/2 in case of maximum value of instantaneus power fo AC wave.V^2 = 10000 in the example 100*100, k , but why divided by twice= 2XL where XL= 1Ohm?
sould not be 10000 W? 100A*100V?tx Henry.

 

[Ratch]

View attachment 19491 Hi. someone may explain me how Maximum Power has been calculated in formula here in the image?
Watt = V*I or V^2/R.or Vmax*Imax/2 in case of maximum value of instantaneus power fo AC wave.V^2 = 10000 in the example 100*100, k , but why divided by twice= 2XL where XL= 1Ohm?
sould not be 10000 W? 100A*100V?tx Henry.

The current existing in the circuit is 100/sqrt(1^2+r^2), where sqrt(1^2+r^2) is the absolute value of the impedance. The power dissipated in the resistor is (I^2)*r , which comes out to( (100/sqrt(1^2+r^2)^2)*r . Taking the derivative with respect to "r" and finding the value of r for the max power, we get r = 1 and r = -1. Rejecting the negative value we know that r has to be 1 in order to obtain the max power. Substituting into the power equation we get( (100/(1^2+1^1)^2)*1 = 5000,

Ratch

 

[e21959]

Hi. Tvm Ratch. I have collected data you told me and put them into wolfram alpha computational engine. yes, you were right. Since i often forget how to calculate derivative( there are a lot of teoremas to remember !!). Did i understand what you told me? am I doing it correctly?

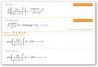
in the 1st image when r = 1 y = 5000 , and in the 2nd one (derivative) global maximum for r = 1 is 5000
And exploring web found this too:

The power factor of the inductor is equal to zero, cosx(phase angle) = 0. Consequently
the complex power absorbed by the inductor has real part equal to zero, as
in the case of the capacitor, and therefore the average power absorbed by the inductor is
equal to zero. The inductor, as the capacitor , it is a bipole conservative and,
therefore, there is no energy dissipation. The reactive power absorbed is positive
and applies

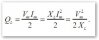
are The same 5000W absorbed as reactive power by the coil ?, Tvm for help Ratch, best Regards

 

[Ratch]

e21958,

You can solve for R analytically for the maximum/minimum value by taking the derivative of the power equation with respect to R, setting the derivative to zero, and solving for R. Since the inductor and resistor are in series, they both pass the same current. Since R's resistance and L's reactance are equal, they will both handle the same power. The resistor will dissipate 5000 watts as heat energy loss, and the inductor will store the energy and give it back to the circuit twice every cycle for an energy loss of zero.

Ratch