Integrator circuit using single resistor gain"ad620" op amp?

[mhf1366]

Hi guys.i am wondering if its possible to use a single resistor gain op amp like "ad620an" in a integrator circuit!
pls help me.
thanks.

 

[KrisBlueNZ]

Hi and welcome to Electronics Point

Yes I think you can, but why would you? There's no advantage; only disadvantages, including the increased cost.

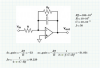
The AD620 is just a differential amplifier with programmable gain. The op-amp integrator circuit requires a differential amplifier with high gain. So set the gain high, and connect the AD620 as the op-amp in the standard integrator circuit (non-inverting input = 0V; resistor from circuit input to inverting input; capacitor from op-amp output to inverting input).

If you try it, let us know how you get on.

 

[mhf1366]

Dear KrisBlueNZ
thanks for your fast reply.
actually i am trying to design a normal rogowski coil and i was thinking if i use a constant gain op amp over a range of frequency (between 100 Hz and 1KHz) then probably the frequency response of my integrator will be constant over this range.
in the AD620 data sheet the gain in this range is constant but the problem is that i was confused about where to put the resistors because i dont know if in this situation i can use the formula for normal integrator.
i will inform you by the results as soon as possible.
thanks again.

 

[LvW]

.............. probably the frequency response of my integrator will be constant over this range.
..........in the AD620 data sheet the gain in this range is constant

1.) The frequency response of an (ideal) integrator is not constant but drops with 20dB/dec.
2.) For good integration prperties the open-loop gain of the used amplifier should be as large as possible (opamp: 1E5...1E6).
In your case - with a fixed gain of max. 10000 - the "intergrator" will behave as a first order lowpass.

Hence, why not using a single opamp?

 

[KrisBlueNZ]

The frequency response of a standard op-amp integrator is set by the resistor and the capacitor. It is assumed that the op-amp has enough gain that errors due to gain are negligible. Using a differential amplifier with relatively low gain will affect the frequency response of the integrator but I couldn't define how. Someone who knows the maths, such as Laplace or Harald or LvW, could quantify the effect it would have. But I don't see how it would be useful.

Are you using a resistor in parallel with the integration capacitor? Just wondering. How do you reset the integrator at the start of the integration period?

 

[LvW]

Integration means: Phase shift of 90 deg Therefore my question: Which accuracy do you require?
More than that, the data sheet contains no information about the gain of 1E4 (frequency response, slew rate).

 

[Arouse1973]

Integration means: Phase shift of 90 deg Therefore my question: Which accuracy do you require?
More than that, the data sheet contains no information about the gain of 1E4 (frequency response, slew rate).

Hi LVW
Phase shift of 90, what at all frequencies?
cheers Adam

 

[KrisBlueNZ]

Guys, look up the Wikipedia article on Rogowski coils. I think he intends to use the integrator as an actual integrator rather than a kind of filter.

 

[LvW]

Hi LVW
Phase shift of 90, what at all frequencies?
cheers Adam

Yes - of course. The ideal integrator function 1/jwT exhibits a magnitude drop of 20 dB/dec and a constant phase of -90 deg (+90 deg for an inverting integrator).
However, a real intergator (based on a real opamp) has a phase characteristic which is near 90 deg and crosses the 90 deg at one single frequency only.
Therefore, my question in post#6.

 

[LvW]

Guys, look up the Wikipedia article on Rogowski coils. I think he intends to use the integrator as an actual integrator rather than a kind of filter.

Yes - but the problem is: It is not possible to realize an (ideal) integrator. It always will be a low pass filter (however, with a rather small corber frequency).

 

[Arouse1973]

Yes - of course. The ideal integrator function 1/jwT exhibits a magnitude drop of 20 dB/dec and a constant phase of -90 deg (+90 deg for an inverting integrator).
However, a real intergator (based on a real opamp) has a phase characteristic which is near 90 deg and crosses the 90 deg at one single frequency only.
Therefore, my question in post#6.

Ah you were talking about an ideal op amp, don't find many of them lying around
Adam

 

[Arouse1973]

Guys, look up the Wikipedia article on Rogowski coils. I think he intends to use the integrator as an actual integrator rather than a kind of filter.

Ah yes this is interesting, so he will be integrating the voltage produced by the coil to give a voltage on the output of the integrator that is proportional to the current in the coil. He will also need a resistor across the capacitor to limit the gain at low frequencies It appears this is commonly capped at 1Hz, not sure what gain he will need I'll see if I can work it out. Also the coil will limit the bandwidth its self so you might only need an opamp with a bandwidth of say a couple of MHz
Adam

 

[Arouse1973]

Here is my attempt as working some of this out. It appears that you don't need as much gain as first thought to process the coils output. Values I have used seem to be a common choice.
Thanks
Adam

 

[Laplace]

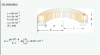
While not of particular interest for the transient signals of Rogowski coils, there is still the question of integration with op-amps having low DC gain. An ideal integrator with infinite gain will have a transfer function of the form '1/s' which gives a ramp output to a step input whereas an integrator with finite gain has a transfer function of the form '1/(s+a)' which gives an exponential output to a step input. Following graph shows parametric curves for integrator output to a step input for selected gain values from 10 to 10,000. Attached pdf shows the derivation.

 

[Arouse1973]

Nice one Laplace. The output of the Rogowski coil is generally very small so we are right down the very bottom left of your graph which is where it's always more linear. And the reduced gain at low frequencies I believe helps with low frequencies interference pickup. So that's why you don't need very large gains at low frequency.
That's how I understand it, might be wrong though.
Adam