-
Categories
-
Platforms
-
Content
You'll need both types of equation and combine them in the right way. Use sum of currents for the top center node, you know the voltage across the network from top to bottom etc.
Once the set of equations has been set up, solve for the unknowns.
Once the set of equations has been set up, solve for the unknowns.
Last edited by a moderator:
You have to apply whatever it needs to set up the system of equations such that you can solve for the unknowns. Sometimes one method or the other may suffice, at other times you'll need both types of equation. There is no general rule.
The numbers are good.
I strongly urge you to always use numbers + units in your equations. For example:
Keeping tabs on the units helps you to verify the plausibility of your equations. If, for example, you come across an equation R=3V/2V you know that this van't be correct becasue the unit of resistance (R) is Ω, which is Volt/Ampere.
I strongly urge you to always use numbers + units in your equations. For example:
I2 = 3/5 ?? µA? mA? A? ...
Keeping tabs on the units helps you to verify the plausibility of your equations. If, for example, you come across an equation R=3V/2V you know that this van't be correct becasue the unit of resistance (R) is Ω, which is Volt/Ampere.
In the same way: set up the equations, solve for R.
Show us your effort.
Also, I will move this thread to the homework section where it belongs, I think.
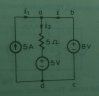
From the circuit, I can't find out the current or voltage across the R because R is unknown
I think the possible conditions
Current through 1Ω
I=50v/1Ω
I=50/1 A
voltage across 1Ω
V=50A*1Ω=50v
Now how to find out current and voltage for 2Ω
Doing a quick calculation shows that this diagram has no single solution. You can express voltage across the 2 Ω resistor and current through it only as a function of R. As in V(2Ω) = f(R).
Or vice versa.
Unless one other current is given. E.g. current through R as indicated by the arrow on the wire leading to R.
Or vice versa.
Unless one other current is given. E.g. current through R as indicated by the arrow on the wire leading to R.
What do you mean?
Arrow is indicate the direction of current, not the value of current. If I apply the kcl at left node of 2 Ohm resistor. I can't set the equations because there are two unknown values of current
You are completely lost. You have an independent voltage source and an independent current source. The R resistor can be any physical value you can name. Unless you specify what the current or voltage is present across or through the resistor, no specific value for R can be calculated.
Ratch
As Ratch elaborated: You can chose any value of R and will get a resulting distribution of currents and voltages whcih can be expressed by a set of equations as in V(2Ω) = f(R) where f(R) is a rational function of R.
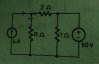
Let's suppose voltage across R is V
Then current throw R resistor should be Ir=V/R
current I1=4A given
Current through the 2 ohm resistor is I2
Apply kcl
I1=Ir+I2
4A=V/R+(V-50)/22
If the current through 1ohm resistor is I3
I4 is current from 50 volt source
Again from the kcl
I2+I4=I3
(V-50)/2+I4=50
Here I have two equations but I don't understand how to solve
Then current throw R resistor should be Ir=V/R
current I1=4A given
Current through the 2 ohm resistor is I2
Apply kcl
I1=Ir+I2
4A=V/R+(V-50)/22
If the current through 1ohm resistor is I3
I4 is current from 50 volt source
Again from the kcl
I2+I4=I3
(V-50)/2+I4=50
Here I have two equations but I don't understand how to solve
You are getting careless in your proofreading.
The I3 current present is 50 amps. After all, it has 50 volts across 1 ohm, doesn't it. You show 2 equations and 3 unknowns. Try to solve for only the voltage V across R, then you can easily find the currents elsewhere in term of R. Hint: Use the superposition method.
Ratch
You already did. 4=V/R+(V-50)/2=====> V=58 R/(2+R). Pick any R and the voltage can be calculated. Do you have a sense of what is going on?
Ratch
Do you mean, the value of R may be anything 2, 4, 8 ohms etc. I have to take one value then I have to find voltage and current through R
I did as you said
If R= 2 ohms then voltage across 2 ohms resistor is 29 volts
Last edited:
Yes, that is correct. The independent current source is going to output 4 amps regardless of what the value of R is. Likewise, the independent voltage source is going to output 50 volts regardless of what R is. All the other resistors are fixed in value. The only way you can change the voltage across R, or the current through R, is to change the value of R. As an extreme case, consider R = 0 . The equation you found gives a voltage value of 0 volts. Makes sense, right? Now, consider R = infinity. The equation gives a value of 58 volts. Once you know the voltage across R, you can find the currents in the rest of the circuit.
Ratch
