help to calculate frequency of CD40106BC schmitt trigger square oscillator

[george2525]

Hello

I am building a synthesiser that uses a basic schmitt trigger square wave oscillator



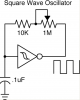
I have found some info that makes sense to me regarding calculating the frequency here:

http://electronics-course.com/schmitt-trigger-oscillator

which states f = 0.8/RC for the 741S14 model.

However im using a Texas CD40106 which has the following datasheet:
chrome-extension://oemmndcbldboiebfnladdacbdfmadadm/http://www.ti.com/lit/ds/symlink/cd40106b-mil.pdf

I have read in a decent book that the oscillation frequency of the CD40106 is approx - 0.75/RC

I have used the same principles to calculate it as shown in the link above however I am unable to obtain anything close to 0.75/RC based on the datasheet values provided.

So... would anyone know how to calculate the oscillation frequency for this IC?

Perhaps I have chosen the wrong values from the datasheet but I have tried a few options

I assumed I would pick temperature at 25C and use the typical values

The datasheet seems to say that output is +10v and 0V if Vdd = 10v and Vcapacitor is between 3.9 and 5.9 volts which I assume means hysteresis should be 2V? however the datasheet states hysteresis at 2.3V! which confuses me...

anyway if anyone is prepared to help Ill explain what ive done further.

Thankyou!

 

[Alec_t]

For a 40106 the frequency will be ~ 1.5/RC if the IC is lightly loaded (i.e. has a feedback resistor which draws < about 1mA).
Bear in mind that datasheet values are "typical". Because of manufacturing tolerances no two ICs will have identical properties. The R and C values also have tolerances, so you shouldn't expect the frequency of your circuit to be exactly as per the formula.

 

[george2525]

For a 40106 the frequency will be ~ 1.5/RC if the IC is lightly loaded (i.e. has a feedback resistor which draws < about 1mA).
Bear in mind that datasheet values are "typical". Because of manufacturing tolerances no two ICs will have identical properties. The R and C values also have tolerances, so you shouldn't expect the frequency of your circuit to be exactly as per the formula.

Thanks for your reply

yes I have found it as 1.5/RC also

would you have any idea where the value 0.75/RC could have come from?

Thanks

 

[BobK]

I expect that you calculated only half the period. There are two halves (charge and discharge) and that would explain the factor of two in the frequency.

Bob

 

[george2525]

I expect that you calculated only half the period. There are two halves (charge and discharge) and that would explain the factor of two in the frequency.

Bob

hmm the 1.5/RC is one period but the 0.75/RC from the book is quoted in Hz so should also be one period. Also the above link with the 74LS14 is 0.8/RC which seems in line with the book statement. There seems to be a 1/2 missing but I cant see where from!

 

[Alec_t]

would you have any idea where the value 0.75/RC could have come from?

As Bob says. However, I got f=1.5/RC by running a simulation with LTspice and measuring the frequency.
The book figure was presumably for TTL logic, not CMOS logic. Frequency is a function of the hysteresis, which is quite different for the two logic technologies.

 

[BobK]

Show us your computation.

Bob

 

[george2525]

Show us your computation.

Bob

ok

ive been messing around with different Vdd's and using the following


which is stated in the datasheet for the Fairchild model

with Vdd = 10v I get fosc = 0.811/RC

and with Vdd = 5v I get fosc = 1.23/RC

I have since found this formula and its derivation and it makes sense to me. the 0.811 seems close to standard quotations.

I would like to ask - is it normal for Vdd to have such an effect on the frequency?

(A nice derivation can be found here)
chrome-extension://oemmndcbldboiebfnladdacbdfmadadm/http://electro-music.com/forum/phpb..._oscillator_with_diode_based_cv_input_905.pdf

 

[george2525]

also I plan to use 9V for Vdd

is there a way to find Vt+ and Vt- without experimentation?

I will be experimenting anyway but would like to know

 

[Alec_t]

is there a way to find Vt+ and Vt- without experimentation?

The datasheet should tell you. For CMOS, Vt+ and Vt- are ratiometric with respect to Vdd. Vt+ is about 65% of Vdd and Vt- is about 35% of Vdd. Your mileage may vary. For TTL, Vt+ and Vt- are about 1.6V and 0.8V respectively.

 

[george2525]

The datasheet should tell you. For CMOS, Vt+ and Vt- are ratiometric with respect to Vdd. Vt+ is about 55% of Vdd and Vt- is about 45% of Vdd. Your mileage may vary. For TTL, Vt+ and Vt- are about 1.6V and 0.8V respectively.

ok but order to generate accurate frequencies I will just have to take a specific schmitt trigger and somehow determine its Vt+ and Vt- right? sorry if that seems obvious but just in case I missed a trick

 

[BobK]

ok but order to generate accurate frequencies I will just have to take a specific schmitt trigger and somehow determine its Vt+ and Vt- right? sorry if that seems obvious but just in case I missed a trick

In order to get accurate frequencies you will have to use a potentiometer for part of the resistance and tune each oscillator. The only way to get accurate frequencies without tuning is to use a crystal.

Bob

 

[george2525]

In order to get accurate frequencies you will have to use a potentiometer for part of the resistance and tune each oscillator. The only way to get accurate frequencies without tuning is to use a crystal.

Bob

OK yes sounds like the best idea. Ill use a trimmer. thanks

 

[Alec_t]

For a non-crystal CMOS oscillator the frequency will drift to some extent with temperature and with supply voltage, which is not ideal for some applications.

 

[AnalogKid]

1. From post #1, 3.9 V and 5.9 V are not symmetrical about Vdd/2. 3.9 V and 6.1 V are, for a delta-V of 2.2 V, much closer to your original information.

2. Internally, the transition voltages hve both a fixed and a ratiometric component. This is why their overall percentages shift as Vdd changes.

3. The P-channel transistors in CMOS parts are not as "good" as the N-channel transistors, so the driving point impedance for the feedback resistor is not symmetrical. For a large resistor it is a small error term, but a good example of how complex the calculation can get when you try to get it to be really accurate.

ak

 

[george2525]

1. From post #1, 3.9 V and 5.9 V are not symmetrical about Vdd/2. 3.9 V and 6.1 V are, for a delta-V of 2.2 V, much closer to your original information.

2. Internally, the transition voltages hve both a fixed and a ratiometric component. This is why their overall percentages shift as Vdd changes.

3. The P-channel transistors in CMOS parts are not as "good" as the N-channel transistors, so the driving point impedance for the feedback resistor is not symmetrical. For a large resistor it is a small error term, but a good example of how complex the calculation can get when you try to get it to be really accurate.

ak

ok so why would the data sheet not quote those figures? I see your point but I would expect the datasheet to cover this. Interestingly for non-Texas models I think I have seen figures like yours. datasheets can be irritating