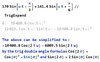Determining the source voltage

[electronicsLearner77]

This the circuit i am trying to solve, I need to find the voltage e1

My work is like
e1 + e2 = v -> Applying the Kirchoff's Voltage Law
e1 = v - e2;

But the answer does not seem to match. What is the mistake?
Note: small clarification, can I use latex here?

 

[Harald Kapp]

What is the mistake?

What is E2? Why would you use an RMS value + angle here? Makes no sense. Use the vectors as given in the task description.

can I use latex here?

Not directly. You can paste an image of a set of equations generated by LaTeX.
Or see this list of BB Codes that allow a bit more text formatting than the menu items above this edit window.

 

[electronicsLearner77]

What is E2?

I am not sure if this is what you are asking. I have represented in phasor notation for E2

Why would you use an RMS value + angle here? Makes no sense. Use the vectors as given in the task description.

Generally all AC circuit analysis is done using phasor notation. Am I correct?

 

[Harald Kapp]

I am not sure if this is what you are asking. I have represented in phasor notation for E2

No. What you show here is e2, but for E2 you use the RMS. Why? That's not correct

e1 + e2 = v -> Applying the Kirchoff's Voltage Law
e1 = v - e2;

Up to this part everything is correct.

 

[bertus]

Hello,

Have a look at this page of the AC book, how to do calculations with AC signals that have different phases:
https://www.allaboutcircuits.com/textbook/alternating-current/chpt-2/examples-ac-circuits/

Bertus

 

[electronicsLearner77]

No. What you show here is e2, but for E2 you use the RMS. Why? That's not correct

But book says for phasors we have to use the RMS values, that is the reason i converted.

And from the examples i followed the same methodology.

 

[Ratch]

Why get snarled up with RMS and phasors? Just subtract the trig expressions and deal with the result later if you want to express it into different views. Now you can transform the above expression into a sin or cos function and multiply/divide by sqrt 2 or anything else you desire. Ratch

 

[electronicsLearner77]

Why get snarled up with RMS and phasors? Ratch

Could you please let me know how to handle below equation

I think it is always easy to go with the method i mentioned, that i hope is the standard followed by all.

 

[Ratch]

To each his own way.
Ratch

 

[electronicsLearner77]

To each his own way.
Ratch
View attachment 49488

I don't want to drag it further, but my point is here we are dealing signals and our topic is electronics and not trigonometry. So solving like a trigonometry problem you miss the signal analysis. This is only my point of view.

 

[Harald Kapp]

Generally all AC circuit analysis is done using phasor notation. Am I correct?

O.K..
But you don't need to convert to RMS for making the calculation and at the end convert back to peak. The first involves division by sqrt(2), the latter multiplication by sqrt(2). Both operations cancel each other. Simply using peak values simplifies the calculation.
As to your error look here:

You use 120.1 /_-60 = 120.2 × (cos(-60) - j sin(-60)) which should imho be 120.1 /_-60 = 120.2 × (cos(-60) + j sin(-60))
You then go on with

In this equation obviously cos(-60) = -1/2 and sin(-60) = -sqrt(3)/2 but cos(-60) is + 1/2, not -1/2

 

[Harald Kapp]

What is your new result? Do you know the expected result?

 

[electronicsLearner77]

Yes, i corrected what you pointed, but one confusion with the final angle calculation. The result is

The magnitude matches with the angle but struggling for the phase angle, i know i have to do some manipulation since the real and imaginary parts are -Ve. What exactly i need to do?
The answer is

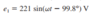
I know some 180 degrees to be subtracted, but not sure of the sequence.

Note: It would really help if you upgrade to Latex editor.

 

[Harald Kapp]

You can see from real and imaginary parts in -26.5 -j × 154 that the phasor points into the 3rd quadrant. Therefore add or subtract 180°. It doesn't matter which ot the two you chose because you'll end with either 160.23 ° or -99,77 ° which is the same (if you don't believe me, draw the diagram).
The result matches closely my calculation (apart from some minor differences due to rounding).

Note: It would really help if you upgrade to Latex editor.

For a very few savvy ones like you: yes. LaTex isn't that common. You can always post an equation created in the favorite tool of your choice (there are others than LaTex, more specialized in primarily typesetting math equations) as an image, as you obviously have done.

 

[electronicsLearner77]

It doesn't matter which ot the two you chose because you'll end with either 160.23 ° or -99,77 ° which is the same

This is really a good point. Thank you. I was breaking my head if i have to add or subtract.

 

[Ratch]

Everybody has the wrong answer. Since all the voltages are in sin(wt) format, we don't have to convert anything. All we have to do is subtract e2 from v to get the answer. Subtracting is the same as flipping the e2 phasor over 180 degrees and adding up all the x-components of phasors v and e2 . Doing so we get -37.456. The y-components add up to -217.924. In polar form, the result is easily found by rectangular coordinate arithmetic to be 221.12/_-99.75525degrees. Any questions?

Ratch