Current Direction

[MJ812]

Hey guys,

I'm fairly new to electronics and I got a couple simple and probably stupid questions. I'm studying programming and I'm attempting to simulate a circuit. I got stuck with coming up with an algorithm to tell if resistors were in series or parallel and decided each component needed to know which way current was flowing, if at all.

So I came up with a couple of scenarios that I need some help with, here's a picture.

So in the first image I have a simple circuit and the question is (dumb I'm sure), Is current flowing on the 2 wire segments in the middle?

In the second image(2 resistors) the same question applies to the wire segments on either side of the switch but which way does the current flow across the switch when it is closed? I assume right to left because of the lower resistance along the perimeter but I'm not sure.

Lastly the third image, the resistance along both paths is the same so what happens across the switch?

Thanks for the help.

 

[(*steve*)]

So in the first image I have a simple circuit and the question is (dumb I'm sure), Is current flowing on the 2 wire segments in the middle?

None

In the second image(2 resistors) the same question applies to the wire segments on either side of the switch but which way does the current flow across the switch when it is closed? I assume right to left because of the lower resistance along the perimeter but I'm not sure.

Anything between none and a very tiny fraction, and it could flow either way.

Lastly the third image, the resistance along both paths is the same so what happens across the switch?

Anything between absolutely nothing and it carrying the entire current (in either direction.

Thanks for the help.

I'm sure it's not much help.


Infinite resistances are easy, but zero resistances often don't make any sense if you place them in parallel. In reality they may not be zero and any small deviation can cause all manner of different behaviour.

 

[MJ812]

Was your answer dependent on the voltage and resistance I used? If so, they are just arbitrary values so i could have some numbers to play with. The main thing I'm trying to grapple is having a component know when current is coming in and when it is going out.

None

I'm trying to conceptualize the physics involved, I'm probably going about this all the wrong way. I can see the electrons moving along the outer wire but are you saying that adjacent electrons in the useless wire are entirely idle?

Anything between none and a very tiny fraction, and it could flow either way.

Anything between absolutely nothing and it carrying the entire current (in either direction.

what determines the amount and direction in these cases?

Infinite resistances are easy, but zero resistances often don't make any sense if you place them in parallel. In reality they may not be zero and any small deviation can cause all manner of different behaviour.

Sorry you've lost me here. I should probably hunt for some decent books huh.

 

[davenn]

I'm trying to conceptualize the physics involved, I'm probably going about this all the wrong way. I can see the electrons moving along the outer wire but are you saying that adjacent electrons in the useless wire are entirely idle?

Yes, the electrons in a wire will only flow where there is a complete circuit
in your first pic with the 2 short wire branches they dont form a complete circuit so there wont be any current flow in them

There is 1 exception to this ... that is if a capacitor is involved
now lets take your first circuit again ... remove the top section of the circuit where you have arrows shown around so that you are left with the lower section with the battery the gap and the resistor.
Put a capacitor in the gap

as you may know and can see the capacitor is essentially a gap in the circuit too
the difference being the capacitor has parallel plates that can be charged up

assumption ... capacitor is initially uncharged

When the switch is closed the there is an initial flow of current as the capacitor charges up
Electrons flow into one plate making that plate negatively charged and they drive electrons away from the other plate, through the resistor and to the battery, leaving that plate positively charged.
Once the capacitor charges up to the voltage of the battery, the current stops flowing.
If the switch is then opened, the capacitor will stay charged ( ignoring long term slow leakage between the plates via the dielectic)

cheers
Dave

 

[KrisBlueNZ]

Your three circuits don't really make sense because no voltage appears across a piece of wire (well, a perfect piece of wire with zero resistance, anyway), so (neglecting the very small resistances of the wire), putting two pieces of wire in parallel, or putting a resistor in parallel with a piece of wire, doesn't have any effect.

In your top left circuit, the two open points marked with question marks are actually at the same voltage. The voltage and the resistor determine the current that flows in the whole loop.

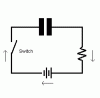
In the top right circuit, your 5 ohm resistor is in parallel with a piece of wire, so it has no effect. The current will be 1.5V / 10 ohms = 150 mA.

That's the current through the battery, and through the 10 ohm resistor.

With the circuit as shown, in the real world, some of that current will flow through the wire at the top, and some will flow through the 5 ohm resistor via the wire that's connected across the open switch.

The 150 mA will be split according to the relative resistances of the two paths. Almost all of it will flow through the wire, and a tiny bit will flow through the resistor.

Assuming that the wire across the top has a resistance of, say, 0.01 ohms, you can calculate the overall resistance of the parallel combination of a 0.01 ohm piece of wire and a 5 ohm resistor using the parallel resistor formula:

1/Rtot = 1/R1 + 1/R2 ...

R1 = 0.01
R2 = 5
so Rtot = 0.00998 ohms.
Almost exactly 0.01 ohms, the resistance of the wire across the top. Putting a 5 ohm resistor in parallel with that piece of wire has only changed the resistance by a tiny amount.

Now if you want to calculate the current through each path, you start with the voltage across the parallel combination, which can be calculated using Ohm's Law. We know the total current is 150 mA, and the resistance is 0.00998 ohms, so the voltage will be V = I R = 1.497 mV.

This voltage causes a current flow in each leg of the parallel combination. For the wire, this is:
I = V / R = 0.001497 / 0.01
= 149.7 mA
For the resistor, this is:
I = V / R = 0.001497 / 5
= 0.3 mA

Those two currents, 149.7 and 0.3 mA, add up to the 150 mA in the rest of the circuit.

Here I've neglected the resistance of the wire in series with the 5 ohm resistor, because it is relatively tiny. I've also neglected the fact that the tiny voltage drop across the wire and the paralleled resistor will increase the total circuit resistance slightly, so the total current will be slightly less than 150 mA.

The current flow in the 5 ohm resistor is negligible in comparison with the current flow in the wire across the top; the point of going through these calculations is to show how insignificant it is, in a way you can comprehend step-by-step.

So connecting a resistor in parallel with a piece of wire does very little to change the resistance of the piece of wire, or to bypass any of the current that would flow through that wire. It's only when you put two resistors with significant resistance in parallel that you need to do any calculations.

In your circuit at bottom left, the battery and resistor current will again be 150 mA, and the current in the top part of the circuit will be split between the wire across the top, and the wire in the middle (the wire that bypasses the switch, and the wire from there to the right side).

As in the second circuit, the current will split according to the relative resistances of the two paths. Assuming they're both made with the same wire and the same length, the current will split evenly. But this is all a bit academic really.

I find a good way to understand voltage, current, resistance, and resistances in series and parallel is my "DTS model". DTS stands for the three quantities:

D: Distance (corresponds to voltage)
T: Tension (corresponds to current)
S: Stretchiness (of a spring) (corresponds to resistance).

A resistor is modelled as a tension spring (or a piece of elastic). "Stretchiness" means the ease with which the spring can be stretched. So a weak spring, made with thin wire, has a high stretchiness, so it's a high resistance; a strong spring made with thick wire has a low stretchiness and low resistance.

If you stretch a spring out to 1.5 feet in length (or use your favourite unit of distance), you are applying 1.5 volts across it, and the tension (force) can be calculated using the equivalent of Ohm's Law:
I = V / R becomes
T = D / S (tension = distance / stretchiness).

Connecting two resistors in series (a voltage divider) is equivalent to hooking two springs together at one point. You're left with the two unattached ends. If you stretch them to a certain distance (apply a voltage across the series combination), each spring will stretch (voltage will appear across it) in proportion to the stretchiness (resistance) of the spring (resistor). The sum of the distances (voltages) across the two springs (resistors) will be equal to the total distance (applied voltage).

Connecting two resistors in parallel is equivalent to hooking two springs together at both ends and stretching them together to a certain distance. Both springs (resistors) have the full distance (applied voltage) across them, but the tension (current) in each spring (resistor) is inversely proportional to its stretchiness (resistance).

The parallel combination of two or more springs is equivalent to a single spring with less stretchiness (resistance) than any of the component springs; the formula, unsurprisingly, is:

1 / total_stretchiness = 1 / spring_1_stretchiness + 1 / spring_2_stretchiness ...

This DTS model is my own idea - at least, I've never seen it anywhere else. It is NOT compatible with the "current as a flow" analogy, nor with any other analogies that might exist!

I hope this helps. Please let me know what you think.

Edit: This is not a perfect explanation of the DTS model. A resistor with no current through it has no voltage across it, whereas a spring that's not being stretched still has a base length, which needs to be ignored. The extension beyond the base length of the spring, and not the total distance, is equivalent to voltage.

 

[gorgon]

Just a little comment. The Arrows in Your drawings are not showing the current flow, but the Electron flow. This is defined to be -I or negative current. The current I is defined to flow from V+ to V- of the battery.

This is important to get correct when you start setting polarity on the current, in calculations.

 

[KrisBlueNZ]

Just a little comment. The Arrows in Your drawings are not showing the current flow, but the Electron flow. This is defined to be -I or negative current. The current I is defined to flow from V+ to V- of the battery.

Are you sure about that gorgon?

Current flow from positive to negative is called "conventional current" and it goes "in the direction of the arrow" on circuit symbols. I prefer to use that model myself as well in schematics and descriptions, and those diagrams certainly do show "electron flow".

But is it really true that "current" is "defined" as conventional current, and it's incorrect to call "electron flow" "current"? Do you have a reference for this definition?

 

[davenn]

thanks for pointing that out, Kris

I was going to call out gorgon on that as well

Dave

 

[MJ812]

Your three circuits don't really make sense

Hah, yeah they weren't supposed to, I was attempting to come up with scenarios where current direction was ambiguous. That being said, I was in the dark about what happens to electrons in the useless wires in the first circuit, I've included another CRUDE image of what I think I understand is going on from what you have said.

I understand where I went wrong with the resistance calculation. I didn't think that current wouldn't even bother going through the 5 ohm resistor (negating resistance of the wires). I included a picture of it too, ignoring wire resistance the inner parts of the circuit would be ignored right?

So I need to do two things, components need to know if the potential is there for current to flow and then i need to parse the circuit to find routes to ground. In the bottom 2 pictures I put the states of the connections of the components. Current could flow through switch C but it's not connected to anything so I could ignore it when doing calculations.

The dilemma is the resistance of the wires and the components themselves. I didn't want to have to include them but although they are 'insignificant', the path of the current makes no sense without them. If switch C was connected to the resistor, I would have to assume that both paths are identical and split the current across them. I could easily come up with situations that make absolutely no sense.

Thanks for the input, lots of learning needed on my part.

Your DTS model makes sense, thanks for sharing.

 

[Laplace]

But is it really true that "current" is "defined" as conventional current, and it's incorrect to call "electron flow" "current"? Do you have a reference for this definition?

I would refer you to the 1952 edition of College Physics by Sears & Zemansky. See section 28-2 The direction of a current. "It would seem logical to define the direction of a current as the direction of motion of the free charges. We immediately come up against the difficulty, however, that in an electrolytic or gaseous conductor free charges of both signs are in motion in opposite directions. Whichever direction was assigned to the current, we would find charges moving in the opposite direction. Since some convention must be adopted, it has been agreed to speak of the direction of any current as if the carriers were all positive charges. Hence in a metallic conductor the electrons move in the opposite direction to the conventional current."

Since electric circuits consist almost entirely of solids, only electrons produce current flow in almost all circuits. But this fact is seldom important in circuit analysis because the analysis is almost always at the current level and not at the charge level.

 

[KrisBlueNZ]

I understand where I went wrong with the resistance calculation. I didn't think that current wouldn't even bother going through the 5 ohm resistor (negating resistance of the wires). I included a picture of it too, ignoring wire resistance the inner parts of the circuit would be ignored right?

Yes, I believe so. As the resistance of the parallel wire approaches zero, the amount of current flowing in the parallel resistor approaches zero as well. I don't know how you would describe the situation when the resistance is actually exactly zero; it depends on how you deal with division by zero, which is something that doesn't interest me, as an engineer rather than a mathematician

So I need to do two things, components need to know if the potential is there for current to flow and then i need to parse the circuit to find routes to ground.

Well, there's nothing special about "ground". In practice at least, for a meaningful current to flow, a non-zero voltage needs to be applied across a non-zero resistance. That just requires a path from the power source.

In the bottom 2 pictures I put the states of the connections of the components. Current could flow through switch C but it's not connected to anything so I could ignore it when doing calculations.

I don't understand the meanings of the 0 and 1 markings on the diagram. They indicate the "states of the connections"? I don't see how... the way the switch is drawn seems to indicate whether it's open or closed. I think my earlier explanations are fairly clear, and I can't add much to them anyway.

The dilemma is the resistance of the wires and the components themselves. I didn't want to have to include them but although they are 'insignificant', the path of the current makes no sense without them. If switch C was connected to the resistor, I would have to assume that both paths are identical and split the current across them. I could easily come up with situations that make absolutely no sense.

Right. I don't know how this problem is dealt with by circuit simulators. One approach I can think of would be to assume that every piece of wire has a ridiculously tiny resistance - for example, 1 x 10^-100 ohms. Calculations will produce crazy interim results, but I think the final results would be meaningful.

There are sure to be other Electronics Point users who can go into detail.

Thanks for the input, lots of learning needed on my part.
Your DTS model makes sense, thanks for sharing.

Cool!

 

[gorgon]

Are you sure about that gorgon?

Current flow from positive to negative is called "conventional current" and it goes "in the direction of the arrow" on circuit symbols. I prefer to use that model myself as well in schematics and descriptions, and those diagrams certainly do show "electron flow".

But is it really true that "current" is "defined" as conventional current, and it's incorrect to call "electron flow" "current"? Do you have a reference for this definition?

Well it looks that my selection of the sole word 'defined' might have been a bit bombastic, and I stand at least partly corrected.
From Wiki:
'A flow of positive charges gives the same electric current, and has the same effect in a circuit, as an equal flow of negative charges in the opposite direction. Since current can be the flow of either positive or negative charges, or both, a convention for the direction of current which is independent of the type of charge carriers is needed. The direction of conventional current is arbitrarily defined to be the same as the direction of the flow of positive charges.'

If the direction of the current is not 'conventional' it should be commented in the drawings, due to the probability of confusion and readability.

 

[MJ812]

Well, there's nothing special about "ground". In practice at least, for a meaningful current to flow, a non-zero voltage needs to be applied across a non-zero resistance. That just requires a path from the power source.

Maybe my understanding of ground is off here, for current to flow through switch C wouldn't it need a path back to the power source? Switch C itself would offer some resistance in reality so wouldn't that suggest that some current would be flowing even though it has nowhere to go? That ties in to my understanding of the useless wires in the first diagram.

I don't understand the meanings of the 0 and 1 markings on the diagram. They indicate the "states of the connections"? I don't see how... the way the switch is drawn seems to indicate whether it's open or closed. I think my earlier explanations are fairly clear, and I can't add much to them anyway.

I'm sure my diagram is to blame here, all switches are normally open, in the first diagram they are open, the input side has a true state because there is a path to it from a power source. In the second diagram the same switches are closed and so the output sides of them now have a path from the power source and then power can also reach the resistor and back to the power source. This way the components can easily tell when they could be receiving power.

Right. I don't know how this problem is dealt with by circuit simulators. One approach I can think of would be to assume that every piece of wire has a ridiculously tiny resistance - for example, 1 x 10^-100 ohms. Calculations will produce crazy interim results, but I think the final results would be meaningful.

Thanks for the suggestion, I may have to use an approach like this, it depends on how redundant or complicated things get the closer I get to a realistic simulation.

Do you have any suggestions for a good starter kit and or tutorials/books? I've used a breadboard before but only using a step by step guide. I'm reading bits and pieces here and there but some practical work would be awesome.

 

[davenn]

Maybe my understanding of ground is off here, for current to flow through switch C wouldn't it need a path back to the power source?

the term ground here is irrelevent
yes it would ... and there isnt one

Switch C itself would offer some resistance in reality so wouldn't that suggest that some current would be flowing even though it has nowhere to go? That ties in to my understanding of the useless wires in the first diagram.

irrelevent, it wouldnt matter it there was 1 Ohm or a million Ohms of resistance ...
you answered this in the part above ... no path back to source

cheers
Dave

 

[KrisBlueNZ]

Well, there's nothing special about "ground". In practice at least, for a meaningful current to flow, a non-zero voltage needs to be applied across a non-zero resistance. That just requires a path from the power source.

Maybe my understanding of ground is off here, for current to flow through switch C wouldn't it need a path back to the power source? Switch C itself would offer some resistance in reality so wouldn't that suggest that some current would be flowing even though it has nowhere to go? That ties in to my understanding of the useless wires in the first diagram.

Yes, it needs a complete circuit, but "ground" is the irrelevant part, as Dave says. "Ground" and "Earth" really mean the soil of this planet, or the Earth pin of an AC mains outlet, which is (supposed to be) connected to the soil via an earth stake.
The words "Ground" and "Earth" are also used to refer to the default reference rail, from which all voltages are measured (unless otherwise specified). This rail is also known as "common" or "0V" ("zero volts"). I prefer to call it 0V.

Most often, the 0V rail is connected to the negative side of the power source for the circuit. Any voltages that are measured at a single point (e.g. "the voltage on U1 pin 3 is 4.5V") are measured relative to ("with respect to") the 0V rail. That's why it's called 0V; because the voltage of the rail itself, measured relative to itself, is always zero volts!

Your diagrams don't have ground, earth, common, or 0V marked on them. The fact that battery negative is usually 0V is not enough; you really should explicitly show your 0V rail. This could be as simple as printing "0V" next to a wire that connects to that node. In a circuit simulator, there is a special symbol that you can connect to the 0V rail of the circuit. With LTSpice, if you don't have one of these connected to your circuit, you get all kinds of errors.

Whether you call it ground, earth, common, or 0V, it has no special significance in terms of controlling current flow. Current can only flow in a complete circuit. Whether part of that circuit is also the reference voltage point, and whether it's connected to the planet, don't affect the requirement for a complete circuit.

Do you have any suggestions for a good starter kit and or tutorials/books? I've used a breadboard before but only using a step by step guide. I'm reading bits and pieces here and there but some practical work would be awesome.

No, sorry. But I would suggest that you play around with other circuit simulators. LTSpice is a free download from http://www.linear.com and it seems to be pretty good, although it has relatively few components - mostly it has Linear Technology ICs and components that are used with them, as you'd expect from a free program provided by Linear Technology

 

[MJ812]

Thanks.

 

[Ratch]

MJ812,
Another long lost soul. To determine directly the true physical direction of electrical current, use an ammeter. It is calibrated to read "conventional" or so called "calculated" current. Reverse what the ammeter direction indicates to get the true physical direction. Same is true for semiconductors. The arrow on a junction diode points in the opposite direction to the true direction of the negative electrons really flowing through it, and the correct direction of the positive hole flow which only occurs within the diode itself and not the external wires.

Ratch

 

[ratstar]

Mj812, i cant see your pictures. but they are excellent for you to figure it out. its not that hard, get off the virtual simulations and test things for real, the simulations on the net are flawed.

if you play with resistors and wires and more than 1 battery at once youll discover->

* voltage division
*current division
* addition
* subtraction

 

[Martaine2005]

This thread is from 2014.
You’re flogging a dead horse.

Martin

 

[Harald Kapp]

Another long lost soul.

Maybe not so. Post #16 is 6 years old
Thread closed to prevent resurrection of a zombie thread.