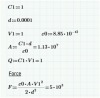Coulomb's Law in practical life!

[vilyanur]

As given in this site: http://electronicspani.com/coulombs-law/

the formula of coulomb's law is:

I understand that! But I have hard time following it practically.

If I place two positive and negative wires carrying one ampere current per second that will result in one coulomb charge in each wire isn't it?

And If I place them in vacuum or air , then I can see that the force of attraction between those two wires should be 9.98 * 10^9 Newton! Isn't that tremendous force? I have never seen two wires carrying one ampere current being attracted with that much of force!

 

[Arouse1973]

Please explain fully how you calculated your final result. This will help us see where you might have gone wrong. If you have at all Oh just to help you a little further, do really think it's realistic to have a stationary charge of 1C, because that is what this formula means.
Thanks
Adam

 

[BobK]

The wires have no net charge. The force between them comes from magnetic force which is a different formula.

Bob

 

[Harald Kapp]

Charge is measured in Coulombs where 1C=1A*1s.
Current is measured in Amperes.
The two are incommensurate, meaning you can't compare them and you cannot replace one for the other in an equation.

1C=1A*1s is the charge that would be stored in a capacitor when a current of 1A flows into the capacitor for 1second.

With respect to the attraction of wires where a current flows, see Bob's answer or read this and this.

 

[vilyanur]

Please explain fully how you calculated your final result. This will help us see where you might have gone wrong. If you have at all Oh just to help you a little further, do really think it's realistic to have a stationary charge of 1C, because that is what this formula means.
Thanks
Adam

If Q1 , Q2 both are one Coulomb and r is also one meter then F becomes 1 / 4 * pi * ε0 * εr
ε0 = 8.854 187 817... x 10−12
http://en.wikipedia.org/wiki/Vacuum_permittivity
and for vacuum εr = 1 so, F = 1 / 4 * pi * ε0 * εr = 8.98 * 10^9
I wrote 9.98 * 10^9 in Original Post mistakenly but 8.98 * 10^9 is still tremendous.

 

[vilyanur]

@ Bobk and Harald

Ok! I understand it now. But I think One Coulomb stationary charge can be found in many capacitors and other charged materials isn't it? But they are not attracted to each other or repelled with such tremendous force!

 

[Harald Kapp]

Why do you think the "plates" of a capacitor are not attracted by a "tremendous" force? The attraction or repulsion of electrostatic forces can be used e.g. by an electrostatic voltmeter where this force visibly displaced a moveable electrode. You do not normally notice this force because the "plates" of a capacitor are constructed from conducting material separated by a very thin insulator. You cannot see how the attractive force operates on the "plates" because they cannot visibly move . the insulator stops any movement.

You can see the repelling force of electrostatic charges e.g. by rubbing a balloon against your hair and watch the strands of hair - having like charges - stand up and seeking to maximize their distance.

 

[Arouse1973]

If Q1 , Q2 both are one Coulomb and r is also one meter then F becomes 1 / 4 * pi * ε0 * εr
ε0 = 8.854 187 817... x 10−12
http://en.wikipedia.org/wiki/Vacuum_permittivity
and for vacuum εr = 1 so, F = 1 / 4 * pi * ε0 * εr = 8.98 * 10^9
I wrote 9.98 * 10^9 in Original Post mistakenly but 8.98 * 10^9 is still tremendous.

Yes but this is for a stationary amount of charge. You need to look at Amperes Law as shown in Harald's Link.

 

[Arouse1973]

@ Bobk and Harald

Ok! I understand it now. But I think One Coulomb stationary charge can be found in many capacitors and other charged materials isn't it? But they are not attracted to each other or repelled with such tremendous force!

When you put a large amount of charge on a capacitor on one side what do you think happens to the other side? Well it pushes the same amount of charge away from the other side. So your net charge is zero, which means no force between the two plates, that's why they don't implode.
Adam

 

[BobK]

No net charge outside the capacitor, but the plates will have equal and opposite charges, so they will attract each other.

Remember though, the for large capacitors, the kind that might hold a Coulomb of charge, this is distributed over a huge area.

Bob

 

[Arouse1973]

Thanks Bob, you learn something everyday.
Ah so a point charge of 1C would have a massive attraction on another point charge of 1C. Is the attraction dependant on distance between the plates? F=(1/2QV)/d if so how do you factor in surface area?
Thanks
Adam

 

[(*steve*)]

Ah so a point charge of 1C would have a massive attraction on another point charge of 1C.

Yes, and the calculation has been done above I believe.

Is the attraction dependant on distance between the plates? F=(1/2QV)/d

Yes. According to that equation it's inversely proportional to distance.

if so how do you factor in surface area?

Divide it by the surface area to get pressure

Large capacitors that are violently discharged can make a sound as the pressure is released.

There are similar forces at work in inductors that can cause them to make sounds. Some are actually designed to do so -- we call them speakers. Have you ever checked out how electrostatic speakers work (they're capacitors)?

Interestingly a description of electrostatic speakers notes that a constant charge must be maintained (as opposed to a constant voltage) because the force is inversely proportional to the charge, but inversely proportional to the square of the voltage (I think).

 

[Arouse1973]

Very informative, I have never done anything with electrostatic speakers. I shall look into this further as this sort of thing interest me greatly.
Cheers
Adam

 

[Arouse1973]

Ok so here's my stab at it. Don't Laugh

Coulombs Law

F = Ke * q1 * q2 / r2
q1 = Charge 1 in coulombsq2 = Charge 2 in coulombs
r = Distance between the two objects in meters
F= Force between the two objects in Newton’s
Ke = Coulomb Constant
Example 1


This is the original assumption made in the first post, where it was assumed that this was the force between two current carrying conductors with 1Amp of current. Here I have tried to work it out properly.

Force between parallel current carrying wires

Take two wires of length L and place them side by side and apply a current in the same direction in both. A force in one will be produced by the magnetic field of the other wire.

When two current carrying wires are separated by a distance a force will be experienced between the two wires. Depending on the direction of current in each wire will depend on whether the force is attractive or repulsive. If the current is flowing in the same direction the wires will attract each other and if the current is in the opposite direction the wires will repel.

Example 2

I1 = current in wire 1 in Amps
I2 = current in wire 2 in Amps
B1= Magnetic field produced by wire 1 in Tesla
B2= Magnetic field produced by wire 2 in Tesla
μ0 = Vacuum permeability
L =Length of wire in meters
F1 = Force on wire 1 in Newton / meters
F2 = Force on wire 2 in Newton / meters



Force between two Parallel plates (Capacitor)

This was another question ask about the force in a capacitor which had +/-1C of charge on the plates.

When a voltage is applied across the plates of a capacitor the capacitor's plates receive a charge of +/- Q. This creates a surface charge density of +/- σ where σ = Q/A (Charge divided by Area).

This in turn produces an electric field between the plates and because the plates are the same the total electric field is Etotal = Q/Aε0 and the potential difference (voltage) between the plates is Etotal * d, where d is the distance between the plates.

Because the plates have opposite charges the force between them is equal to the electric field produced by one plate multiplied by the charge on the other. Which is?

F= Q*(Q/2 Aε0 ) =(ε 0AV2)/2d^2)

When two parallel plates with opposite charges are brought close enough together to form a conventional capacitor the electric field between the two inner surfaces add together. But the electric fields on the outside of the two plates cancel. This is where I think the term net charge of zero comes from for a so called charged capacitor. But there is still an attraction between the inner plates of the capacitor as pointed out by BobK, thanks Bob.

Example 3
C1 = Capacitance in Farads
d = distance between the plates in meters
ε0 =Vacuum permittivity
V1 =Voltage across the capacitor
Q = Charge in Coulombs
A = Area of one plate in m^2


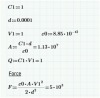
So you can see that the forces are not as high as first assumed and that the surface area of a 1F capacitor which will hold 1C of charge with a potential difference of 1V with just two plates is very large. And when this original 9 billion Newton’s is spread over such a large surface area it’s force is reduced substantially.
Thanks
Adam

 

[Ratch]

As given in this site: http://electronicspani.com/coulombs-law/

the formula of coulomb's law is:

I understand that! But I have hard time following it practically.

If I place two positive and negative wires carrying one ampere current per second that will result in one coulomb charge in each wire isn't it?

And If I place them in vacuum or air , then I can see that the force of attraction between those two wires should be 9.98 * 10^9 Newton! Isn't that tremendous force? I have never seen two wires carrying one ampere current being attracted with that much of force!

That is the formula for two point charges separated by a distance. If you want the force of a point and a line of charge, or a point and a plane of charge, that is a different formula. Ratch

 

[(*steve*)]

Specifically, the force between two lines of charge is linear with distance, and between two planes of charge, is independent of distance.

The last of these is a particularly interesting one.

Noe that both require mathematical lines and planes (i.e. unbounded), but apply approximately while the distance between the charges is small compared to their linear dimensions.