2nd order PLL simulation

[NickS]

Hello all I am new to your forum but it looks to be a great resource.

I am trying to implement a 2nd order PLL for my OQPSK receiver simulation(in Matlab)
But I think there is a flaw in my documentation though I am not sure.

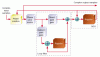
the Block diagram:

eta[n] --->(Phase Detector)--e[n]-->(filter 1)---c[n]--->(filter 2)---->phi[n]
                     |                                               |
                      ------------------( e^j )<---------------------

filter 1 = KL*( 1 + alpha * z^-1 ) / ( 1 -z^-1 )
filter 2 = mu * z^-1 / ( 1 -z^-1 )

Which seems to make sense but I don't think the example code follows this block diagram
EXAMPLE CODE:

Ts = 1/fs2;
mu = Ts;
BL = 10; %loop bandwidth
zeta = .707; %damping factor
wn = 2*BL/(zeta+1/(4*zeta)); %natural frequency
KL = wn^2*Ts+2*zeta*wn; %filter constant
alpha = -2*zeta/(2*zeta+wn*Ts); %filter constant
c1 = 0; e1 = 0; %these denote c[n-1] and e[n-1] respectively
phi = zeros(size(eta)); %empty vector the same size as input eta
eta = -eta;
for n = 2:length(eta)
   e = eta(n-1)*conj( exp(j*phi(n-1)) ); %phase detector
   c = KL*mu*(e + alpha * e1) + c1; %filter 1 ?
   phi(n) = c+phi(n-1); %filter 2 ?
   c1 = c;
   e1 = e;
end

So I don't think the variables c or phi are properly calculated to the block diagram. Can anyone fresh on Z transforms please confirm or reject my suspicions.

Thanks
-Nick-

 

[NickS]

Well I don't believe that I have asked a terribly difficult question to an experianced SWR engineer so perhaps it would help my cause to say that I am not doing this for homework.

I graduated 2 years ago with my BSEE and my focus has been in hardware design. I recently have been required to simulate a simple OQPSK system since I know matlab reasonably well. I did find this example in a textbook by I can't make the loop lock. If I replace(almost all of it) and do a more dirrect phase comparison to find the error and simply replace the filters with a single scaled correction I can make the thing lock for a phase error but I need the second order property to be able to compensate for frequency as well.

Any advice would be appreciated.
-Nick-

 

[55pilot]

Demanding an answer is usually not a good way to get volunteers to help you.

---55p

 

[NickS]

Sorry if my tone seemed demanding. I noticed that many post was being viewed but not replied to and thought I knew the reason for being passed over. I figured I was being shunned because I was asking a question that(admittedly) looks like it could be homework.

Having read the sticky in the locked homework section just thought I had to better clarify my intent. But it was not my intent to demand.

My apologies to all that I have offended.

I am just glad now that someone besides me has said something in this thread.

 

[Ian]

It could just be that although people have viewed it, there hasn't been anyone able to provide a detailed enough answer (or don't have time to reply at the moment). I've not used matlab for many years, so I'm not able to help in this case.

Hopefully someone will spot this that is familiar with what you are asking . Welcome to the site

 

[Mitchekj]

Yeah, sorry. I have no idea. I figured no post was more constructive than an "I don't know" post.

 

[NickS]

...Welcome to the site

Thanks. I have been looking for this sort of forum since my university based engineering forum went down last year.

I am talking to a software radio guru tonight so I will post what I learned tomorrow.

Nick

 

[NickS]

I ended up using a common variant on the standard PLL called a Costas loop(still second order) It works great

The block diagram is attached.
The block diagram is defined thusly

theta(n+1) = theta(n) + alpha*e(n) + f(n)
f(n+1) = f(n) + beta*e(n)

theta = phase correction (NCO register)
alpha = filter gain 1
beta = filter gain 2
f = frequency offset (loop filter register)
e = phase error

The filter coefficients are chosen based on your needs but a good starting place is
alpha = .01
for critical damping beta = (alpha^2)/4
for over damping beta < (alpha^2)/4
for under damping beta > (alpha^2)/4

Since I used OQPSK I had to cheat slightly on my phase estimation. Since my I and corresponding Q bits are offset by Tb/2 I can not just sample one point determine I and Q and map it to the constellation for phase estimate. So I use I(n) with Q(n+Tb/2) for a single phase estimate. But when applying the correction factor theta it has to be to the time aligned sequence.

All that said here is the way I implemented it and hopefully this post will save somebody out there some time like it would have me.

IQpll = sampIQrx(startPoint:endPoint); %BB signal  2samp/sym [I(1),Q(1),I(2),Q(2),I(3)...]
bits = length(IQpll)/2; % number of complex symbols
alpha = .03; 
beta = alpha^2/4; %critical damped

e = zeros(1,bits); %initialize error vector
theta = zeros(1,bits); %initialize phase correction vector
dfc = zeros(1,bits); %initialize frequency offset vector

theta(1) = PhaseEst; %starting point (converges faster for non-zero first estimate)
dfc(1) = FreqEst*2*pi/28.8e3; %starting point (converges faster for non-zero first estimate)

for n = 2:length(theta)
    Ipll = real(IQpll(2*(n-1)-1)*exp(1i*theta(n-1))); %apply correction
    Qpll = imag(IQpll(2*(n-1))*exp(1i*theta(n-1)));%apply correction
    angSh = mod( -angle(Ipll + (Qpll*1i)),pi/2); % shift symbol to 1st quadrant
    e(n) =(angSh -(pi/4)); %rotate by pi/4 and the value is your phase error
    
    dfc(n) = dfc(n-1) + beta * e(n-1); %loop filter calculation
    theta(n) = theta(n-1) + (alpha*e(n-1)) + dfc(n-1); %phase calculation 
    if abs(theta(n))>pi
        theta(n) = theta(n)-2*pi*sign(theta(n));% handles phase wrapping
    end

    II(n-1) = Ipll; %used I sample
    QQ(n-1) = Qpll; %used Q sample

end

Note that in the presence of no frequency offset dfc converges to 0 and theta converges to the phase offset. In the presence of frequency offset dfc converges to the frequency offset and theta never converges but does maintain a constant slope when locked.

I find it useful to plot e, theta, and dfc after the loop is done running.

-Nick-